Algorithme HITS |
 |
Petit rappel
Il est possible que vous sentiez le besoin de revoir le texte sur les vecteurs et matrices de la première semaine avant de lire le présent texte. Si c’est le cas, n’hésitez pas à le revoir.
Hub-and-Authority
PageRank mesure l’importance relative d’une page sur le web.
Bien que ce soit une mesure importante, on pense parfois
qu’elle ne permet pas de découvrir des pages qui sont
des « autorités » (références) dans un domaine particulier.
Le modèle de Kleinberg,
à la différence de PageRank, distingue les « authorities » (pages recevant
beaucoup de liens) des « hubs » (pages contenant beaucoup de liens vers
de bonnes pages). Il est possible pour une page d’être les deux
à la fois, mais certaines pages peuvent n’être qu’une bonne page
de contenu ou n’être qu’une bonne liste de liens.
Algorithme HITS : version simplifiée
Voici comment fonctionne l’algorithme HITS. Soit la requête d’un
utilisateur notée ![]() .
.
- On fait d’abord une recherche classique (en utilisant par exemple un modèle vectoriel avec tf.idf). On note les pages trouvées les plus pertinentes,
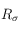 [1].
[1]. - À partir de l’ensemble des pages trouvées
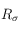 , on construit un plus grand ensemble
, on construit un plus grand ensemble 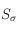 qui contient :
qui contient :
— les pages qui contiennent des liens vers [2]
[2]
— les pages qu’on trouve à partir d’un lien sur une page se trouvant dans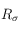 .
. - Une fois que
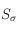 et
et 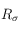 sont trouvés, on peut calculer la mesure « authority » (
sont trouvés, on peut calculer la mesure « authority » (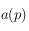 ) ainsi que la mesure « hub » (
) ainsi que la mesure « hub » (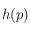 ) pour chaque page
) pour chaque page 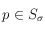 . La mesure « authority » quantifie la qualité de la page en tant que page qui reçoit des liens, alors que la mesure « hub » quantifie le statut de la page en tant que page de liens.
. La mesure « authority » quantifie la qualité de la page en tant que page qui reçoit des liens, alors que la mesure « hub » quantifie le statut de la page en tant que page de liens.
On fixe d’abord ![]() et
et ![]() pour tout
pour tout ![]() . On note
. On note ![]() la condition « q contient un
la condition « q contient un
lien pointant vers p ». On effectue alors les trois opérations suivantes en séquence, les répétant autant
de fois que nécessaire, jusqu’à ce que les valeurs ![]() et
et ![]() convergent vers des valeurs stables.
convergent vers des valeurs stables.
-
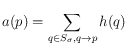 (une bonne page de contenu obtiendra beaucoup de liens de la part de bonnes pages de liens) ;
(une bonne page de contenu obtiendra beaucoup de liens de la part de bonnes pages de liens) ; -
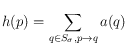 (une bonne page de liens pointe vers de bonnes pages de contenu) ;
(une bonne page de liens pointe vers de bonnes pages de contenu) ; -
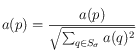 ,
, 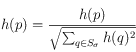 (on normalise
(on normalise 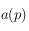 et
et 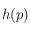 de manière à ce que la somme de leurs valeurs au carré soit unitaire).
de manière à ce que la somme de leurs valeurs au carré soit unitaire).
On peut ainsi trouver les pages qui sont des « autorités » quant à la requête de l’utilisateur. Il suffit d’offrir à l’utilisateur les pages ayant le meilleur score ![]() .
.
Notons que, contrairement à PageRank, le calcul de ![]() est fait pour chaque requête de l’utilisateur ! C’est donc évidemment plus coûteux et complexe.
est fait pour chaque requête de l’utilisateur ! C’est donc évidemment plus coûteux et complexe.
Reprenons l’exemple que nous avions utilisé pour l’algorithme PageRank.
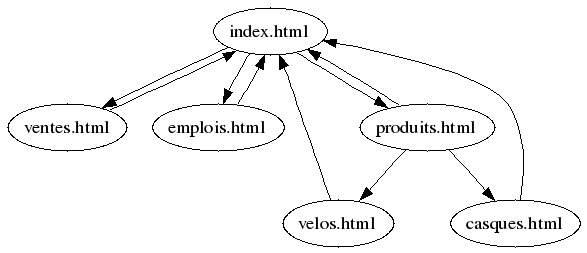
Soit les pages avec leur description :
- index.html pointe vers 3 pages (ventes.html, emplois.html, produits.html) ;
- produits.html pointe vers 3 pages (velos.html, casques.html, index.html) ;
- emplois.html pointe vers une page (index.html) ;
- ventes.html pointe vers une page (index.html) ;
- velos.html pointe vers une page (index.html) ;
- casques.html pointe vers une page (index.html).
Supposons que, à la suite d’une recherche, disons celle de « rabais postal sur vélo », j’obtienne comme pages correspondantes seulement la page « velos.html ». Il me faut alors ajouter toutes les pages qui font des liens vers « velos.html » et les pages qui reçoivent des liens en provenance de « velos.html ». J’obtiens finalement l’ensemble suivant :
- index.html pointe vers produits.html ;
- produits.html pointe vers velos.html et index.html ;
- velos.html pointe vers une page (index.html).
Définissons alors la matrice ![]() par
par ![]() si
si ![]() et par
et par ![]() autrement. J’utilise le convention suivante : la première colonne correspond à la page « index.html », la seconde colonne correspond à la page « produits.html », et la troisième colonne correspond à la page « velos.html ». J’obtiens
autrement. J’utilise le convention suivante : la première colonne correspond à la page « index.html », la seconde colonne correspond à la page « produits.html », et la troisième colonne correspond à la page « velos.html ». J’obtiens
Je fixe préalablement ![]() ,
, ![]() ,
, ![]() . J’obtiens que
. J’obtiens que
Et ensuite, on observe que pour calculer ![]() à partir de
à partir de ![]() , il suffit de prendre la transposée de
, il suffit de prendre la transposée de ![]() , comme ceci :
, comme ceci :
Après ces deux étapes, je dois normaliser [3] :
On répète ensuite une seconde fois. Je calcule d’abord ![]() à partir de
à partir de ![]()
puis ![]() à partir de
à partir de ![]()
Et ainsi de suite.
Si je répète cette itération 10 fois, j’obtiens : ![]() et
et ![]() . L’algorithme HITS inciterait donc notre utilisateur à visiter d’abord la page « index.html » et ensuite, seulement, la page « velos.html ». La page « produits.html » ne serait pas recommandée. Pour expliquer ce résultat, on considère le sous-graphe suivant :
. L’algorithme HITS inciterait donc notre utilisateur à visiter d’abord la page « index.html » et ensuite, seulement, la page « velos.html ». La page « produits.html » ne serait pas recommandée. Pour expliquer ce résultat, on considère le sous-graphe suivant :
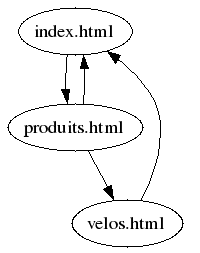
On voit que la page « index.html » reçoit plus de liens que toute autre page ce qui explique, en partie, qu’on la recommande d’abord.
Le théorème suivant montre que si on continue d’appliquer l’algorithme, les valeurs de ![]() et
et ![]() vont converger vers des valeurs uniques.
vont converger vers des valeurs uniques.
Théorème. Les valeurs de ![]() et
et ![]() convergent.
convergent.
En pratique, sur de petits ensembles, il est souvent suffisant de n’utiliser qu’une dizaine d’itérations.
Algorithme HITS avancé : des liens de divers types
Tous les liens ne sont pas égaux. Kleinberg propose de ne pas tenir compte des liens qui sont internes à un site. On peut aussi leur accorder un poids moindre dans les calculs. On peut aussi tenir compte des mots avoisinant le lien. Par exemple, si à proximité du lien on trouve le mot chien, et que la requête de l’utilisateur portait sur les chiens, justement, alors le lien en question est peut-être plus « fort » et devrait recevoir un poids supérieur. Nous ne décrirons pas en détail ces diverses variantes.
Tester l’algorithme HITS
Le moteur de recherche ask.com est basé sur l’algorithme HITS. Vous pouvez aller y faire des recherches et comparer les résultats avec ceux du moteur Google qui est basé sur PageRank.
Référence
– J. Kleinberg. Authoritative sources in a hyperlinked environment. Proc. 9th ACM-SIAM Symposium on Discrete Algorithms, 1998.
[1] $R$ pour « ensemble-racine » ou root, en anglais.
[2] Ce nombre peut être très élevé et, en pratique, on ne choisira qu’un sous-ensemble de toutes ces pages.
[3] $1^2+3^2+2^2=14$



![A=
\left [ \begin{array}{llllll}
0 & 1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array} \right ]. A=
\left [ \begin{array}{llllll}
0 & 1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array} \right ].](local/cache-TeX/43f3c2e32988aab472e5e5eb1e4b63d5.png)
![a(p) = \sum_{q \in S_\sigma, q\rightarrow p} h(q)\left [ \begin{array}{lll}
a(1) & a(2) & a(3)
\end{array} \right ]=
\left [ \begin{array}{llllll}
0 & 1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array} \right ]
\left [ \begin{array}{l}
1 \\
1 \\
1
\end{array} \right ]=\left [ \begin{array}{l}
2 \\
1 \\
1
\end{array} \right ]. a(p) = \sum_{q \in S_\sigma, q\rightarrow p} h(q)\left [ \begin{array}{lll}
a(1) & a(2) & a(3)
\end{array} \right ]=
\left [ \begin{array}{llllll}
0 & 1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array} \right ]
\left [ \begin{array}{l}
1 \\
1 \\
1
\end{array} \right ]=\left [ \begin{array}{l}
2 \\
1 \\
1
\end{array} \right ].](local/cache-TeX/539d6fd5557254fa91f92494945f0ae5.png)
![\left [ \begin{array}{lll}
h(1) & h(2) & h(3)
\end{array} \right ]= A^T \left [ \begin{array}{l}
2 \\
1 \\
1
\end{array} \right ]=
\left [ \begin{array}{llllll}
0 & 1 & 0 \\
1 & 0 & 1 \\
1 & 0 & 0
\end{array} \right ]
\left [ \begin{array}{l}
2 \\
1 \\
1
\end{array} \right ]=\left [ \begin{array}{l}
1 \\
3 \\
2
\end{array} \right ]. \left [ \begin{array}{lll}
h(1) & h(2) & h(3)
\end{array} \right ]= A^T \left [ \begin{array}{l}
2 \\
1 \\
1
\end{array} \right ]=
\left [ \begin{array}{llllll}
0 & 1 & 0 \\
1 & 0 & 1 \\
1 & 0 & 0
\end{array} \right ]
\left [ \begin{array}{l}
2 \\
1 \\
1
\end{array} \right ]=\left [ \begin{array}{l}
1 \\
3 \\
2
\end{array} \right ].](local/cache-TeX/fad0ee66b157f819595fd4053d47d8fa.png)
![a =
\left [ \begin{array}{llllll}
0 & 1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array} \right ]
\left [ \begin{array}{l}
1/\sqrt{14} \\
3/\sqrt{14} \\
2/\sqrt{14}
\end{array} \right ]=\left [ \begin{array}{l}
5/\sqrt{14} \\
1/\sqrt{14} \\
3/\sqrt{14}
\end{array} \right ], a =
\left [ \begin{array}{llllll}
0 & 1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array} \right ]
\left [ \begin{array}{l}
1/\sqrt{14} \\
3/\sqrt{14} \\
2/\sqrt{14}
\end{array} \right ]=\left [ \begin{array}{l}
5/\sqrt{14} \\
1/\sqrt{14} \\
3/\sqrt{14}
\end{array} \right ],](local/cache-TeX/6400db7308c7add0efc05c32e95317ff.png)
![h =
\left [ \begin{array}{llllll}
0 & 1 & 0 \\
1 & 0 & 1 \\
1 & 0 & 0
\end{array} \right ]
\left [ \begin{array}{l}
5/\sqrt{14} \\
1/\sqrt{14} \\
3/\sqrt{14}
\end{array} \right ]=\left [ \begin{array}{l}
1/\sqrt{14} \\
8/\sqrt{14} \\
5/\sqrt{14}
\end{array} \right ]. h =
\left [ \begin{array}{llllll}
0 & 1 & 0 \\
1 & 0 & 1 \\
1 & 0 & 0
\end{array} \right ]
\left [ \begin{array}{l}
5/\sqrt{14} \\
1/\sqrt{14} \\
3/\sqrt{14}
\end{array} \right ]=\left [ \begin{array}{l}
1/\sqrt{14} \\
8/\sqrt{14} \\
5/\sqrt{14}
\end{array} \right ].](local/cache-TeX/deac9ab1491943f0a3f3e36d4bb389a4.png)
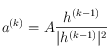 et
et 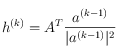 . Ainsi,
. Ainsi, 
