Modèles de langue |
 |
Motivation
On peut traiter un texte comme un « sac de mots » mais la pratique nous révèle que, pour ce faire, il est utile d’avoir un « modèle de la langue », c’est-à-dire un modèle basé sur l’analyse des n-grammes.
Une façon simple de construire un tel modèle est d’estimer la fréquence des bigrammes, ce qui nous permettrait, par exemple, de trouver que la phrase « Jean beau porte » n’a pas de sens en français parce que le bigramme « beau porte » est très improbable.
Comme exemple d’application d’un modèle de la langue, notons qu’il est utile, en recherche d’informations, de faire l’étiquetage des catégories syntaxiques (Part-Of-Speech Tagging en anglais), c’est-à-dire qu’il faut distinguer les noms, les verbes, les adjectifs, les prépositions, les pronoms, les conjonctions et les interjections. On peut aussi vouloir distinguer les nombres des couleurs, etc.
Une autre application des modèles de langue est la traduction automatique qui peut être utile en recherche d’informations si tous les textes ne sont pas écrits dans la même langue. Par exemple, si on tente de traduire en français dog house de façon naïve, on arrivera peut-être à chien maison, mais une analyse statistique sur les bigrammes nous apprendra que dog house se traduit généralement par niche.
Nous avons aussi vu dans le premier module un exemple d’application simple des modèles de langue : on peut déterminer dans quelle langue est écrit un texte en considérant la fréquences des n-grammes le constituant. Par exemple, le trigramme de caractères « the » est fréquent en anglais, mais rare en français.
Définition probabiliste
Un modèle de langue est un concept probabiliste. Quelle est la probabilité que les mots « cacaouette pirouette pas de chance » apparaissent dans un texte donné ? Si nous avons un modèle de la langue, nous saurons le dire au moins approximativement.
Le modèle le plus simple consiste à calculer la probabilité de trouver les mots cacaouette, pirouette, pas, de et chance si on choisit un mot au hasard dans des textes en français. Dans ce cas, on pourra dire que la probabilité associée à l’expression « cacaouette pirouette pas de chance » est :
On peut aussi travailler avec des probabilités conditionnelles plus sophistiquées.
Étant donné une séquence observée de mots comme « cacaouette pirouette », quelle est la probabilité qu’ils soient suivis du mot pas ? On note cette probabilité ![]() .
.
On peut calculer les probabilités assez facilement si on a un grand ensemble de documents (un corpus) par la méthode de vraisemblance maximale. Il suffit simplement de trouver toutes les occurrences du bigramme « cacaouette pirouette » et de voir combien de fois le bigramme est suivi du mot pas, et de faire le ratio « nombre de trigrammes « cacaouette pirouette pas » » sur « nombre de trigrammes commençant par « cacaouette pirouette » ». Si le corpus est vraiment très grand, cette estimation sera fiable.
Lissage
L’estimation des probabilités par vraisemblance maximale a ses limites : quand il s’agit d’estimer de nombreuses probabilités avec une grande quantité d’exemples, mais non infinie, il y aura toujours des problèmes, parfois systématiques.
Dans les faits, il y aura toujours des expressions qui sont correctes et comprises, mais qui ne figurent pas dans un corpus, même très grand. Prenons la phrase : « Jean aime aggraver ceci ou cela. » Quelle est la probabilité de trouver le trigramme « aime aggraver ceci », même dans un corpus très important ? Malgré le fait que ce soit une expression parfaitement correcte, c’est une expression improbable.
On veut donc que notre calcul de probabilité n’associe pas une valeur nulle à un des n-grammes qui n’apparaît pas dans le corpus.
Par exemple, on peut utiliser le lissage de Laplace où on ajoute « 1 » au nombre d’occurrences de tous les n-grammes. En d’autres mots, on prend pour acquis qu’avant même de consulter le corpus, tout n-gramme apparaît au moins une fois. S’il y a trop de mots ou de n-grammes qui n’apparaissent pas ou peu dans le corpus, le lissage de Laplace devient inefficace parce que tous les mots ont pratiquement la même probabilité : 1 sur le nombre de mots. D’autres techniques plus sophistiquées peuvent être utilisées [1]. La technique la plus célèbre étant celle de Good-Turing, parce qu’elle fut utilisée durant la Deuxième Guerre mondiale pour décrypter les communications allemandes. Pour d’autres exemples et des travaux récents sur la question, voir l’article « Question de probabilités... » dans la revue Info Sciences.
La formule de Good-Turing remplace la fréquence d’un élément observé ![]() fois par
fois par ![]() où
où ![]() et
et ![]() sont le nombre d’éléments distincts observés
sont le nombre d’éléments distincts observés ![]() et
et ![]() fois. Pour calculer la probabilité, on procède ensuite comme on le fait avec la vraisemblance maximale. Cette formule fonctionne bien quand nous avons beaucoup de données.
fois. Pour calculer la probabilité, on procède ensuite comme on le fait avec la vraisemblance maximale. Cette formule fonctionne bien quand nous avons beaucoup de données.
En résumé. Si vous observez 4 fois le bigramme « la vie » dans un texte comptant 40 bigrammes, vous estimerez, par vraisemblance maximale, qu’un bigramme sur 10 est « la vie ». Les bigrammes qui n’apparaissent pas dans ce texte se voient accorder une probabilité nulle. Supposons que votre vocabulaire comporte 500 bigrammes ; la technique de Laplace associera alors plutôt une probabilité de (4+1)/(40+500)=1 % à ce bigramme et une probabilité de 0.1 % à tout bigramme qui n’est pas présent dans votre texte. D’autres techniques, comme celle de Good-Turing, donnent des résultats différents qui peuvent être plus ou moins valables selon le cas. Si on suppose que tous les bigrammes furent observés une seule fois, sauf « la vie » qui fut compté 4 fois, alors la formule de Good-Turing accorde une probabilité nulle au bigramme « la vie » (parce que ![]() ) et aussi aux autres bigrammes observés (parce que
) et aussi aux autres bigrammes observés (parce que ![]() ). Par contre, tous les bigrammes non observés obtiennent une fréquence de Good-Turing égale à 40/(500-40) pour une probabilité de 1/(500-40).
). Par contre, tous les bigrammes non observés obtiennent une fréquence de Good-Turing égale à 40/(500-40) pour une probabilité de 1/(500-40).
Les modèles de langue en recherche d’informations
On a vu comment, étant donné un modèle probabiliste, on peut calculer la probabilité d’un texte donné. On peut utiliser cette technique pour déterminer si un texte est en français ou pas, et ainsi de suite.
Il y a un lien direct avec la recherche d’informations. Prenons cette fois-ci la requête de l’utilisateur (par exemple, une suite de mots) comme étant le « corpus », et calculons la probabilité des divers documents à partir de ce modèle.
Par exemple, si la requête de l’utilisateur ![]() est « cacaouette pirouette », nous avons que les mots cacaouette et pirouette sont très probables. Supposons qu’il y a 50 mots possibles dans la langue française [2]. On a donc, avec le lissage de Laplace, 50 occurrences par défaut avec les 2 occurrences dans la requête. Tous les mots, sauf cacaouette et pirouette, ont une probabilité de
est « cacaouette pirouette », nous avons que les mots cacaouette et pirouette sont très probables. Supposons qu’il y a 50 mots possibles dans la langue française [2]. On a donc, avec le lissage de Laplace, 50 occurrences par défaut avec les 2 occurrences dans la requête. Tous les mots, sauf cacaouette et pirouette, ont une probabilité de ![]() , alors que les mots cacaouette et pirouette ont une probabilité de
, alors que les mots cacaouette et pirouette ont une probabilité de ![]() .
.
Supposons que la requête est constituée d’un ensemble de termes ![]() . Le modèle de Hiemstra et al. propose que l’on calcule ensuite la pertinence du document comme suit :
. Le modèle de Hiemstra et al. propose que l’on calcule ensuite la pertinence du document comme suit : ![]() . Par le théorème de Bayes, nous avons
. Par le théorème de Bayes, nous avons 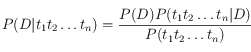 . On suppose que la probabilité de la requête,
. On suppose que la probabilité de la requête, ![]() , est une constante inconnue
, est une constante inconnue ![]() qui ne dépend pas du document ; en supposant l’indépendance de l’occurrence des termes, nous avons
qui ne dépend pas du document ; en supposant l’indépendance de l’occurrence des termes, nous avons ![]() .
.
On peut calculer ![]() par vraisemblance maximale :
par vraisemblance maximale : 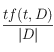 où
où ![]() est le nombre de mots dans le document [3] et
est le nombre de mots dans le document [3] et ![]() est le nombre de fois que le terme
est le nombre de fois que le terme ![]() apparaît dans le document
apparaît dans le document ![]() . On peut aussi fixer
. On peut aussi fixer 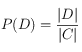 où
où ![]() est le nombre de mots contenus dans tous les documents.
est le nombre de mots contenus dans tous les documents.
Nous avons donc, comme modèle simple, 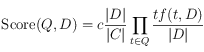 .
.
Exemple. Pour illustrer cette version simplifiée du modèle de Hiemstra et al., considérons la requête ![]() « cacaouette pirouette ». Supposons que nous avons plusieurs documents (totalisant 1000 mots) dont un seul contenant les deux termes (cacaouette et pirouette). Ce dernier document contient les mots « Dans ma pirouette, j’ai perdu ma cacaoutette ». Si un document ne contient pas les deux termes, alors
« cacaouette pirouette ». Supposons que nous avons plusieurs documents (totalisant 1000 mots) dont un seul contenant les deux termes (cacaouette et pirouette). Ce dernier document contient les mots « Dans ma pirouette, j’ai perdu ma cacaoutette ». Si un document ne contient pas les deux termes, alors ![]() pour au moins un
pour au moins un ![]() et le score sera nul. Par contre, si on retient le seul document contenant les deux termes, nous avons que peu importe le terme
et le score sera nul. Par contre, si on retient le seul document contenant les deux termes, nous avons que peu importe le terme ![]() ,
, ![]() . Nous avons que
. Nous avons que ![]() car il y a 8 mots dans le document. Le score sera donc
car il y a 8 mots dans le document. Le score sera donc ![]() ou
ou ![]() pour le document contenant les deux termes et 0 pour les autres documents.
pour le document contenant les deux termes et 0 pour les autres documents.
Le modèle proposé par Hiemstra et al. est en fait plus sophistiqué et estime la valeur de ![]() , à la fois avec la valeur calculée à partir du document
, à la fois avec la valeur calculée à partir du document 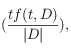 mais aussi avec la valeur calculée à partir du corpus (
mais aussi avec la valeur calculée à partir du corpus (![]() ) de façon similaire à ce que nous avons décrit précédemment.
) de façon similaire à ce que nous avons décrit précédemment.
Grands modèles de langue
Un grand modèle de langage (abrégé LLM de l’anglais large language model) est un modèle de langage possédant un grand nombre de paramètres (généralement de l’ordre du milliard de poids ou plus). Ces modèles sont des réseaux de neurones profonds entraînés sur de vastes quantités de texte. Voici quelques points clés sur les grands modèles de langage :
– BERT (Bidirectional Encoder Representations from Transformers) : Développé par Google en 2018, BERT est l’un des premiers modèles linguistiques influents. Il est conçu pour la compréhension contextuelle des mots et des phrases, mais il n’est pas guidé ou génératif.
– XLNet : Apparu en 2019, XLNet est basé sur l’architecture Transformer. Il améliore BERT en utilisant une approche autorégressive, ce qui lui permet d’obtenir de meilleures performances dans certaines tâches.
– GPT-3 (Generative Pre-trained Transformer 3) : Développé par OpenAI, GPT-3 est l’un des plus grands modèles de langage avec 175 milliards de paramètres. Il excelle dans une variété de tâches, allant de la traduction automatique à la génération de texte créatif.
– T5 (Text-to-Text Transfer Transformer) : T5, également d’OpenAI, est un modèle qui traite toutes les tâches de traitement du langage naturel comme des tâches de traduction de texte. Il a été formé sur un large éventail de tâches et peut être fine-tuné pour des tâches spécifiques.
Ces grands modèles de langue ont révolutionné le domaine du traitement du langage naturel, permettant aux machines de comprendre et de générer du texte de manière similaire à celle des humains. Leur succès a changé l’attention de la recherche vers le traitement du langage naturel, passant des modèles spécialisés supervisés à ces modèles massifs de langage.
[1] Voir, par exemple, Always Good Turing : Asymptotically Optimal Probability Estimation par
Alon Orlitsky, Narayana P. Santhanam et Junan Zhang.
[2] Je fais cette hypothèse parce que, autrement, le lissage de Laplace ne fonctionne pas aussi bien.
[3] Dans le document "La vie est la vie", il y a 5 mots, même s’il n’y a que trois mots distincts.




