

Algorithmique

Motivation
Il ne suffit pas seulement de trouver la bonne information, il faut aussi effectuer la recherche le plus rapidement possible. Vous devez donc être à même de différencier un algorithme lent d’un algorithme rapide. Plus généralement, vous devez avoir une intuition de ce qui rend un programme informatique rapide ou lent. Les bons programmeurs développent généralement une bonne intuition, mais, heureusement, il n’est pas essentiel d’être un programmeur expérimenté pour savoir reconnaître un programme efficace !
Avertissement. Il n’est pas nécessaire, dans ce cours, de devenir un expert en théorie de la complexité ou en performance des logiciels. Seul un aperçu et une compréhension globale sont nécessaires. En cas de doute, vérifiez que vous pouvez mener à terme l’activité d’autoévaluation.
Définitions de base
Un algorithme est une « procédure systématique visant à résoudre un problème ou à atteindre une fin donnée, en particulier par un ordinateur ». La programmation de la solution d’un programme passe généralement par la conception (implicite ou explicite) d’un algorithme.
Par exemple, si on veut afficher le contenu d’une matrice à l’écran, on va parcourir toutes les composantes une à une et effectuer une opération (« print ») sur chaque composante. Il s’agit d’un exemple simple d’algorithme.
Pour un problème comme celui du tri en ordre alphabétique d’une liste de termes, on peut recourir à plusieurs algorithmes différents. Certains algorithmes seront plus rapides, d’autres plus lents.
Comment alors comparer, dans l’absolu, les algorithmes entre eux ? On pourrait, bien sûr, mettre en oeuvre différentes approches et comparer leur vitesse relative, une méthode parfaitement valable que l’on doit souvent adopter. Cependant, cette approche a ses limites sur le plan scientifique : on sait que différents programmeurs peuvent être plus ou moins astucieux ou expérimentés et adopter une approche plutôt qu’une autre. Il est tout simplement très difficile de comparer des algorithmes sur la base d’implémentations parce qu’elles peuvent varier en qualité.
On désire donc une approche mathématique qui nous dise, avec précision, si tel ou tel algorithme est plus lent ou plus rapide qu’un autre. En pratique, la vitesse, au sens strict du terme, n’est pas une quantité qu’on peut mesurer sans implémentation. Par contre, on peut compter le nombre d’opérations que fait un algorithme. Par exemple, l’algorithme suivant fait exactement n opérations :
Pour chaque élément de l'ensemble {1,...,n}:
afficher l'élémentOn associera donc cet algorithme avec la fonction $f(n)= n$, c’est-à-dire qu’on compte le nombre d’opérations effectuées en fonction de la taille de l’ensemble sur lequel on travaille.
Ce qui nous intéresse c’est le comportement de l’algorithme lorsque la taille de l’ensemble augmente ; il faut alors se rappeler le principe selon lequel les algorithmes doivent surtout être rapides lorsque les ensembles de données sont importants. Par exemple, pour $n$ petit, faire $5n$ opérations est plus lent que faire $n^2$ opérations, mais pour $n$ grand, le contraire est vrai. En pratique, on va sans doute préférer l’algorithme qui ne fait que $5n$ opérations parce que pour $n=100$, on fait alors 500 opérations contre 10 000 opérations pour l’algorithme menant au calcul de $n^2$ opérations.
La stratégie généralement employée est donc de comparer les algorithmes lorsque $n$ est très grand et de ne retenir que celui qui fait le moins d’opérations.
Malheureusement, la taille de l’ensemble n’est pas le seul facteur qui détermine le nombre d’opérations que va effectuer un algorithme. Par exemple, si on demande de trier les valeurs dans un vaste tableau dont les valeurs ont déjà été ordonnées, un algorithme de tri pourra s’exécuter plus rapidement que si les données sont pêle-mêle. Mais pour simplifier les choses dans ce cours, nous choisirons toujours le pire cas possible. Soyons pessimistes !
Définition
On cherche maintenant à regrouper les algorithmes dans de grandes classes. Le principe de base est que $n$ et $5n$ sont des classes similaires : faire 5 fois plus d’opérations, peu importe la taille de l’ensemble de données initial, importe beaucoup moins que la différence qu’il peut y avoir entre $n$ et $n^2$.
Définition. Soit $f(n)$ le nombre d’opérations effectuées par un algorithme ; on dit que le temps mis par l’algorithme est $O(g(n))$ (ou bien $f(n) \in O(g(n))$) et cela, s’il existe deux nombres $M$ et $n_0$ tels que $f(n) \leq M g(n)$ pour $n>n_0$.
Premier exemple pour comprendre la définition. Si $f(n)= 2n+5$, on a $f(n)\in O(n)$. En effet, si on pose $M=3$ et $n_0=5$, alors $f(n)=2n+5 \leq M n$ pour $n>n_0$.
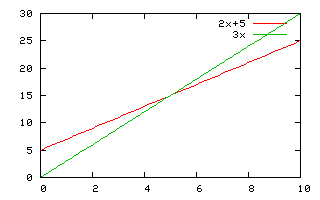
Deuxième exemple pour comprendre la définition. Si $f(n)= 2n+5$, on a $f(n)\in O(n^2)$. En effet, si on pose $M=1$ et $n_0=3$, alors $f(n)=2n+5 \leq M n^2$ pour $n>n_0$.
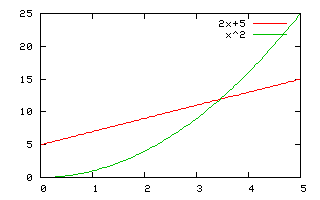
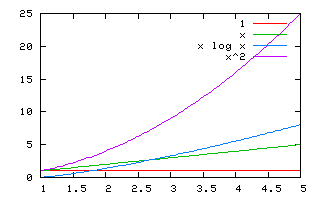
Les grandes classes importantes pour ce cours sont $O(1)$, $O(\log n)$, $O(n)$, $O(n \log n)$ et $O(n^2)$. Les algorithmes en temps $O(1)$ sont très rapides alors que les algorithmes en temps $O(n^2)$ sont les plus lents. Nous avons $O(1)\subset O(\log n) \subset O(n) \subset O(n \log n) \subset O(n^2)$. Par exemple, tous les algorithmes en temps $O(n)$ sont aussi en temps $O(n \log n)$ et $O(n^2)$.
Quelques exemples :
– $n \in O(n)$, en effet, $n \leq n$ pour $n>1$.
– $n \in O(n^2)$, en effet, $n \leq n^2$ pour $n>1$.
– $n^2 \in O(n^2)$, en effet, $n^2 \leq n^2$ pour $n>1$.
– $n \in O(n \log n)$, en effet, $n \leq n \log n$ pour $n>1$. [1]
– $n \log n \in O(n^2)$, en effet $n \log n \leq n^2$ pour $n>1$.
– $n^2 \notin O(n)$, car il n’est pas possible pour $M n$ d’être plus grand que $n^2$ lorsque $n$ est grand, peu importe la constante $M$. En effet, $M n \geq n ^2 \Rightarrow M \geq n$ : alors $M$ est constant et $n$ croît, ce qui constitue une contradiction.
– $n^2 \notin O(n \log n)$, car il n’est pas possible pour $M n \log n$ d’être plus grand que $n^2$ lorsque $n$ est grand, peu importe la constante $M$. En effet, $M n \log n \geq n^2 \Rightarrow M \geq n/(\log n)$ et $n/(\log n)$ sont une fonction croissante.
– $n \log n \notin O(n)$, car il n’est pas possible pour $M n $ d’être plus grand que $n \log n$ lorsque $n$ est grand, peu importe la constante $M$. En effet, $M n \geq n \log n \Rightarrow M \geq \log n$.
Exemple 1
Supposons que nous cherchions la position d’un terme dans un texte et que le texte comporte $n$ mots. Un algorithme simple pour résoudre ce problème pourrait consister à chercher le mot en consultant chaque mot un à un jusqu’à ce qu’il soit trouvé. Quel sera le temps d’exécution de cet algorithme ? En conservant notre étiquette de pessimiste, nous supposerons que le mot recherché est à la fin du texte ; il faudra donc $n$ opérations avant de trouver le mot en question. L’algorithme s’exécute donc en temps $O(n)$.
Exemple 2
Calculer la somme des composantes d’un vecteur est un problème qui se résout en temps $O(n)$.
L’implémentation suivante est une boucle de longueur $n$ :
float sum = 0.0f;
for(int k = 0; k < v.length; ++k)
sum+= v[k];Exemple 3
Trier un tableau peut se faire en temps $O(n \log n)$ si on utilise l’algorithme Merge Sort (tri par fusion). Sun Microsystems utilise l’algorithme Merge Sort dans son implémentation de l’API Java (voir:paquetage java.util).
Voici un exemple de code Java qui se fait en temps $O(n \log n)$ si $n$ est la taille du tableau v :
Arrays.sort(v);Exemple 4
Un algorithme de tri plus simple comme l’algorithme Bubble Sort (tri par permutation) s’exécute en temps $O(n^2)$ plutôt qu’en temps $O(n \log n)$.
Voici un exemple de code Java implémentant Bubble Sort :
void tri(int a[]) {
for (int i = a.length; --i>=0; ) {
boolean drapeau = false;
for (int j = 0; j<i; j++) {
if (a[j] > a[j+1]) {
int T = a[j]; a[j] = a[j+1]; a[j+1] = T;
drapeau = true;
}
}
if (!drapeau) { return; }
} Exemple 5
La décomposition en valeurs singulières d’une matrice de taille $n$ par $n$ se fait en temps $O(n^3)$. L’inversion d’une matrice $n$ par $n$ et la multiplication de deux matrices $n$ par $n$ se font en temps $O(n^3)$ [2].
Exemple 6
Supposons que nous ayons un tableau de valeurs triées, $a_0,a_2,\ldots,a_m$. On peut chercher la valeur $x$ en temps $O(\log m)$ avec l’algorithme de la recherche binaire. Il suffit d’abord de considérer l’élément $a_{m/2}$ puis, si $x> a_{m/2}$, on continue à chercher dans $a_{m/2},\ldots, a_m$, sinon on cherche dans $a_{0},\ldots, a_{m/2}$ et ainsi de suite. Chaque fois, on trouve le point milieu de l’ensemble des valeurs et on poursuit la recherche (dans la bonne moitié). Voici un exemple de code Java :
public static int rechercheBinaire(int[] a, int key) {
int low = 0;
int high = a.length - 1;
while (low <= high) {
int mid = (low + (high-low)/2);
int midVal = a[mid];
if (midVal < key)
low = mid + 1;
else if (midVal > key)
high = mid - 1;
else
return mid; // trouvé!
}
return -(low + 1); // pas trouvé!
}Exemple 7
Il arrive qu’on veuille stocker des clés et des valeurs dans une structure de données. Par exemple, on peut vouloir faire un bottin téléphonique :
| Jean | (432) 432-0444 |
| Marie | (432) 432-0446 |
| Pierre | (432) 432-0447 |
Un problème commun en informatique est qu’on veut récupérer le numéro de téléphone à partir du nom, sans visiter tous les numéros de téléphones chaque fois (ce qui prend un temps $O(n)$ très coûteux).
Heureusement, deux classes Java faisant partie de l’API de base existent pour nous permettre de résoudre ce problème avec peu d’effort. Les deux classes en question diffèrent légèrement dans leur degré de performance selon qu’il soit important ou non de pouvoir retrouver les clés dans un ordre trié. Dans ces classes, deux méthodes sont importantes, la méthode put permet d’ajouter un numéro de téléphone (« put("Jean", "(432) 432-0444") ») alors que la méthode get permet d’en retrouver un (« get("Jean") »).
La classe TreeMap dans l’API Java utilise un arbre rouge-noir pour le stockage de clés et de valeurs. Selon la documentation de Sun, les méthodes containsKey, get, put et remove s’exécutent en temps $O(\log n)$. En comparaison, la classe Java HashMap assure un temps de requête (get et put) en temps constant ($O(1)$), car elle repose sur une table de hachage. Le résultat net est que si on désire des requêtes très rapides, la classe HashMap est sans doute préférable ; cependant, la classe TreeMap permet d’itérer sur les clés en ordre croissant, alors que HashMap énumère les clés dans le désordre.
| Classe | Complexité (performance) | Clés en ordre trié |
| TreeMap | O(log n) | oui |
| HashMap | O(1) | non |
Problèmes NP-difficiles
On pense que tous les problèmes ne peuvent être résolus en temps polynomial, c’est-à-dire qu’ils ne sont pas tous dans une classe $O(n^p)$ pour un certain $p$. On pense qu’il existe des problèmes qui ne peuvent être résolus qu’en temps exponentiel comme $O(2^n)$, mais personne n’en est certain parce qu’il est très difficile de prouver que personne ne pourrait trouver un algorithme plus efficace que celui que nous connaissons à ce jour. Mais l’ingénuité humaine peut parfois être surprenante !
Exemple 1
Le problème de la somme du sous-ensemble est un exemple de problème difficile dont il est facile de vérifier la solution. Soit un ensemble d’entiers tel que $\{1,-1,2,2,\ldots\}$ ; on doit vérifier s’il existe un sous-ensemble dont la somme est 0 (telle que $\{-1,1\}$ dans notre exemple). La taille de l’ensemble est le paramètre $n$. Actuellement, personne ne sait résoudre ce problème en temps polynomial et vous deviendriez célèbre du jour au lendemain si vous arriviez à écrire une solution qui résout ce problème en temps polynomial ! Tellement célèbre qu’on vous offrirait peut-être un poste de professeur d’informatique à Harvard ou à Stanford.
Une fois qu’une solution est fournie, on peut en vérifier l’exactitude en temps $O(n)$ : vous devriez être facilement capable d’écrire un tel programme : il suffit de vérifier que la somme de valeurs données est bien nulle.
Le problème de la somme du sous-ensemble est un exemple de problème qui est de classe NP-difficile.
On peut penser qu’un problème en temps polynomial est plus facile à résoudre qu’un problème NP-difficile, mais il faut cependant se rappeler que certains problèmes qu’on peut résoudre en temps polynomial sont néanmoins extrêmement difficiles. Par exemple, un algorithme en temps quadratique ($O(n^2)$) deviendra rapidement très coûteux en temps de calcul si $n$ est très grand. C’est d’autant plus vrai pour un algorithme dont le temps de calcul progresse selon $n^{10}$. Comme $n$ est souvent très important, on souhaite se limiter le plus possible à des algorithmes qui peuvent au moins se résoudre en temps quadratique ou mieux, en temps linéaire ($O(n)$).
Temps d’accès aux données et temps de calcul
Toutes les opérations effectuées par une machine ne prennent pas nécessairement un temps de résolution égal, contrairement au modèle utilisé par la théorie de la complexité. Il faut se rappeler que ce n’est qu’un modèle théorique qui n’explique pas tout.
Par exemple, un ordinateur moderne peut faire des millions d’opérations de calcul pendant la lecture d’un segment sur un disque. En général, pour écrire des programmes efficaces, on doit tenter de réduire le plus possible le temps de lecture sur les disques. L’utilisation de la mémoire est aussi un facteur déterminant pour minimiser le temps d’exécution d’un programme. La plupart des ordinateurs disposent de mémoire tampon très rapide, mais en petite quantité, ce qui fait qu’on peut facilement traiter très rapidement de petites structures de données, mais beaucoup moins facilement de grosses structures. En d’autres termes si, sur papier, la lecture séquentielle d’un tableau de $10^9$ composantes devrait être $1000$ fois plus lente que la lecture d’un tableau de $10^6$ composantes, la réalité est tout autre et la lecture du tableau de $10^9$ composantes pourrait prendre 2000 fois plus de temps (au lieu de 1000 fois). Un algorithme qui est plus lent sur papier peut donc se révéler beaucoup plus rapide en pratique s’il utilise moins de mémoire et s’il accède moins souvent aux données.
Lectures complémentaires
– Les articles de Wikipédia sur les Notations de Landau, la Complexité algorithmique et la Théorie de la complexité.
– Notation grand-O
[1] Nous utilisons toujours le logarithme en base 2 en informatique.
[2] Il existe des algorithmes sophistiqués qui peuvent faire l’inversion d’une matrice ou la multiplication de deux matrices en temps $O(n^2.376)$, mais c’est un résultat plutôt théorique ; voir les travaux de Don Coppersmith et Shmuel Winograd à ce sujet.

