Vecteurs et matrices |
 |
Motivation
Il est courant en recherche et en filtrage d’informations d’utiliser des vecteurs et des matrices. Nous procéderons donc à un rappel de quelques notions sur le sujet. Il est possible que vous ne soyez pas familier avec certains concepts plus avancés comme la décomposition en valeurs singulières : il ne sera pas nécessaire, dans ce cours, de faire des calculs matriciels sophistiqués, surtout qu’il est plus pratique d’utiliser des algorithmes informatiques pour réaliser ces opérations, mais vous devez en comprendre les concepts.
Je vous invite à lire le présent texte avec attention, à faire le travail d’autoévaluation de la semaine et à revenir périodiquement à cette page lorsque vous en sentirez le besoin.
Note : Si vous ne vous sentez pas capable de faire ces activités mathématiques, nous vous recommandons de vous inscrire au cours de mise à niveau MAT 1000 ou tout autre cours comparable, avant de suivre le présent cours et de faire des études complémentaires. Si vous avez omis de faire les mathématiques du collégial, incluant un cours sur l’algèbre linéaire, soyez conscient qu’un cours d’appoint ne fera que vous donner des bases. Vous devrez sans aucun doute faire du travail supplémentaire par vous-même pour vous mettre à niveau. Nous cherchons à vous aider, mais soyez conscient que c’est de votre responsabilité de maîtriser les notions pré-universitaires nécessaires.
Ensemble
L’ensemble des nombres réels, incluant les nombres à virgule flottante, est noté $\mathbb{R}$ alors que l’ensemble des entiers est noté $\mathbb{Z}$. Les décimales peuvent être notées à l’anglaise avec un point comme dans cet exemple : $2.5$.
Valeur absolue
Étant donné $x \in \mathbb{R}$ ou $x \in \mathbb{Z}$, alors $\vert x \vert = x$ si $x \geq 0$ et $\vert x \vert = -x$ si $x < 0$.
Nombres complexes
Dans le cadre de ce cours, nous éviterons de traiter les nombres complexes. Nous rappelons tout de même leur notation : si $z$ est un nombre complexe satisfaisant $z= x + iy$ où $x,y\in \mathbb{R}$, alors $\vert z \vert = \sqrt{x^2 + y^2}$.
Vecteur
Qu’est-ce qu’un vecteur ? À toutes fins utiles, en informatique, un vecteur est un tableau à une dimension comme dans cet exemple :
$V = \left [ \begin{array}{c}1 \\ 2 \\ 1\end{array} \right ]. $
On dit que ce vecteur a 3 composantes. En mathématiques, on note $V_{i}$ la $i^{\textrm{e}}$ composante du vecteur $V$. Dans notre exemple, $V_1=1$.
En informatique, un vecteur peut contenir des entiers, des booléens, etc. En Java, on peut définir un vecteur comme ceci :
float[] v = {1, 3, 5};ou
float[] v = new float[3];
v[0] = 1;
v[1] = 3;
v[2] = 5.Pour obtenir plus de détails et voir le point de vue des mathématiciens et des physiciens, je vous invite à visiter la page consacrée aux vecteurs dans l’encyclopédie Wikipédia.
Addition de vecteurs et de scalaires
Par convention, si on additionne un vecteur et un scalaire, le scalaire est ajouté à toutes les composantes du vecteur. Avec cet exemple,
$V = \left [ \begin{array}{c}1 \\ 2 \\ 1\end{array} \right ], $
nous avons
$V-1 = V+ (-1)= \left [ \begin{array}{c}0 \\ 1 \\ 0\end{array} \right ]. $
Matrice
En informatique, une matrice est un tableau à deux dimensions ayant $m$ rangées et $n$ colonnes comme dans cet exemple :
$\left [ \begin{array}{cc}1 & 3 \\ 2 & 5 \\ 1 & 5\end{array} \right ]. $
En mathématiques, on note $M_{i,j}$ la valeur se situant à la $i^{\textrm{e}}$ rangée et à la $j^{\textrm{e}}$ colonne de la matrice $M$. Dans l’exemple précédent, $M_{2,1}$ vaut 2 alors que $M_{1,2}$ vaut 3. Une matrice peut contenir des entiers, des nombres réels, des booléens, etc.
En Java, on peut définir une matrice comme ceci :
float[][] m = new float[3][2];
m[0][0] = 1; m[0][1] = 3;
m[1][0] = 2; m[1][1] = 5;
m[2][0] = 1; m[2][1] = 5;Wikipedia présente une discussion plus élaborée sur ce qu’est une matrice.
Multiplication d’un vecteur ou d’une matrice par un scalaire
Dans le cas où les composantes d’un vecteur ou d’une matrice sont des entiers ou des nombres réels (un « scalaire »), on peut multiplier respectivement le vecteur ou la matrice par un entier ou un nombre réel. La multiplication s’applique alors à chaque composante comme dans cet exemple :
$2 \left [ \begin{array}{c}1 \\ 2 \\ 1\end{array} \right ] = \left [ \begin{array}{c}2 \\ 4 \\ 2\end{array} \right ].$
Multiplication de vecteurs et de matrices
Étant donné une matrice $M$ ayant $m$ rangées et $n$ colonnes et un vecteur $V$ ayant $n$ composantes, la multiplication de $M$ et de $V$, notée $M V$, est un vecteur $R$ ayant $m$ composantes et défini comme :
$R_i = \sum_{k=1,\ldots,n} M_{i,k} V_k$
Voici un exemple :
$\left [ \begin{array}{cc} 1 & 3\\ 1 & 2 \\ 3 & 1 \end{array}\right ] \left [ \begin{array}{c} 1 \\ 1 \end{array}\right] = \left [ \begin{array}{c} 4 \\ 3 \\ 4 \end{array}\right]. $
En Java, on calcule la multiplication de deux vecteurs ainsi :
float[][] m = new float[3][2];
m[0][0] = 1; m[0][1] = 3;
m[1][0] = 2; m[1][1] = 5;
m[2][0] = 1; m[2][2] = 5;
float[] v = {1, 3};
// on va maintenant multiplier m et v
float[] r = new float[3];
for(int i = ; i < r.length; ++i)
for(int k = ; k < v.length; ++k)
r[i] += m[i][k]*v[k];
// c'est tout!Il faut un total de $m \times n$ opérations pour multiplier une matrice et un vecteur, c’est-à-dire que le temps de calcul est approximativement proportionnel à la taille de la matrice. Il faudra donc 100 fois plus de temps pour multiplier une matrice $100\times 100$ avec un vecteur que pour multiplier une matrice $10 \times 10$ avec un vecteur.
Multiplication de matrices avec d’autres matrices
Étant donné une matrice $M$ ayant $m$ rangées et $n$ colonnes et une autre matrice $P$ ayant $n$ rangées et $r$ colonnes, la multiplication de $M$ et de $P$, notée $M P$, est un vecteur $R$ ayant $m$ rangées et $r$ colonnes et défini comme :
$R_{i,j} = \sum_{k=1,\ldots,n} M_{i,k} P_{k,j}$
Voici un exemple :
$\left [ \begin{array}{cc} 1 & 3\\ 1 & 2 \\ 3 & 1 \end{array}\right ] \left [ \begin{array}{cc} 1 & 1 \\ 1 & 0 \end{array}\right] = \left [ \begin{array}{cc} 4 & 1\\ 3 & 1 \\ 4 & 3 \end{array}\right]. $
On peut voir la multiplication d’une matrice et d’un vecteur comme un cas particulier de la multiplication d’une matrice par une matrice dans le sens où un vecteur est une matrice ayant une seule colonne.
La transposée d’une matrice
La transposée d’une matrice $M$, notée $M^t$, est tout simplement une réécriture de la matrice où les colonnes deviennent des rangées et vice versa : $M_{i,j}=M^t_{j,i}$. On peut montrer que $(AB)^t=B^tA^t$.
$\left [ \begin{array}{cc} 1 & 3\\ 1 & 2 \\ 3 & 1 \end{array}\right ]^t = \left [ \begin{array}{ccc} 1 & 1 & 3\\ 3 & 2 & 1 \end{array}\right]. $
La transposée est une opération inversible, car la transposée de la transposée d’une matrice est la matrice elle-même : $A^T^T=A$.
Formule. Étant donné deux matrices $A$ et $B$, alors $(AB)^T= B^T A^T$.
Matrice symétrique
Une matrice est symétrique si $A= A^T$. En particulier, pour n’importe quelle matrice $A$, la matrice $A A^T$ est symétrique puisque $(A A^T)^T= A^T^T A^T$.
Matrice normale
Une matrice carrée est dite normale si elle commute avec sa transposée : $MM^t= M^tM$. Par exemple, cette matrice n’est pas normale [1] :
$\left [ \begin{array}{cc} 1 & 1 \\ 0 & 2 \\ \end{array}\right ]. $
En effet, nous avons
$\left [ \begin{array}{cc} 1 & 1 \\ 0 & 2 \\ \end{array}\right ] \left [ \begin{array}{cc} 1 & 0 \\ 1 & 2 \\ \end{array}\right ] = \left [ \begin{array}{cc} 2 & 2 \\ 2 & 4 \\ \end{array}\right ] $
et aussi
$ \left [ \begin{array}{cc} 1 & 0 \\ 1 & 2 \\ \end{array}\right ] \left [ \begin{array}{cc} 1 & 1 \\ 0 & 2 \\ \end{array}\right ] = \left [ \begin{array}{cc} 1 & 1 \\ 1 & 5 \\ \end{array}\right ]. $
Par contre, la matrice suivante est normale :
$\left [ \begin{array}{cc} 1 & 2\\ 2 & 3 \\ \end{array}\right ]. $
En effet, il suffit de vérifier que dans ce cas particulier, $M=M^t$ et donc, $M M^t= M^2= M^t M$.
Une matrice symétrique est automatiquement normale puisque $A^T=A$.
Matrice diagonale et identité
Une matrice carrée est diagonale si seules les composantes sur la diagonale sont différentes de zéro : $M_{i,j}=0$ lorsque $i\neq j$.
Une matrice diagonale est égale à sa transposée : $M = M^t$. Une matrice diagonale est nécessairement normale.
Cette matrice est diagonale :
$\left [ \begin{array}{ccc} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 3 \end{array}\right ]. $
Lorsque la matrice est diagonale et que toutes les valeurs différentes de zéro sont unitaires, on dit qu’il s’agit d’un matrice identité (notée $I$).
La matrice suivante est une matrice identité :
$\left [ \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right ]. $
La multiplication d’une matrice par la matrice identité la laisse inchangée : $M I = I M$.
Matrice inverse
Si $M$ et $P$ sont deux matrices carrées satisfaisant $MP= I$, alors $PM=I$ ; on dit que les matrices sont inverses l’une de l’autre et on note $M= P^{-1}$ ainsi que $P=M^{-1}$. Toutes les matrices n’ont pas un inverse. Vous n’aurez pas à calculer l’inverse d’une matrice dans ce cours.
Vous pouvez vérifier que
$\left [ \begin{array}{cc} 1 & 1 \\ 0 & -1 \\ \end{array}\right ]^{-1}= \left [ \begin{array}{cc} 1 & 1 \\ 0 & -1 \\ \end{array}\right ]. $
La matrice suivante n’a pas d’inverse :
$\left [ \begin{array}{cc} 1 & 0 \\ 0 & 0 \\ \end{array}\right ]. $
Formule. Étant donné deux matrices inversibles $A$ et $B$, alors $(AB)^{-1}= B^{-1} A^{-1}$.
Une matrice qui n’est pas carrée peut néanmoins avoir un inverse par la gauche ou par la droite : si $M$ n’est pas carrée, il peut exister $P$
tel que $MP=I$ ou $PM=I$ (mais pas les deux). Voici un exemple :
$ \left [ \begin{array}{ccc} -2 & 3 & 0\\ 1 & -1 & 0 \\ \end{array}\right] \left [ \begin{array}{cc} 1 & 3\\ 1 & 2 \\ 3 & 1 \end{array}\right ] = \left [ \begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]. $
On utilise souvent la matrice inverse pour résoudre des équations linéaires. Ainsi, étant donné un matrice $A$ et un vecteur $b$, si on a $Ax=b$, alors $x= A^{-1}b$. Cependant, il est possible que le problème $Ax=b$ ait une solution même si $A$ n’est pas inversible comme dans cet exemple :
$\left [ \begin{array}{cc} 1 & 0 \\ 0 & 0 \\ \end{array}\right ] x = \left [ \begin{array}{c} 1 \\ 0 \\ \end{array}\right ]. $
(Une solution possible est : $x = \left [ \begin{array}{c} 1 \\ 0 \\ \end{array}\right ] $.)
Toutes les matrices, mêmes les matrices qui ne sont pas carrées ou qui n’ont pas d’inverse, ont une matrice pseudo-inverse qui permet de trouver la meilleure solution (au sens des moindres carrés) pour l’équation $Ax=b$. On peut calculer la matrice pseudo-inverse en utilisant la décomposition en valeurs singulières (voir le texte plus bas).
Ainsi, la matrice pseudo-inverse de
$A=\left [ \begin{array}{cc} 2 & 0 \\ 0 & 0 \\ \end{array}\right ] $
est tout simplement
$\left [ \begin{array}{cc} 1/2 & 0 \\ 0 & 0 \\ \end{array}\right ]. $
Pour résoudre l’équation $\left [ \begin{array}{cc} 2 & 0 \\ 0 & 0 \\ \end{array}\right ] x= \left [ \begin{array}{c} 1 \\ 0 \\ \end{array}\right ]$, il suffit de calculer :
$\left [ \begin{array}{cc} 1/2 & 0 \\ 0 & 0 \\ \end{array}\right ]\left [ \begin{array}{c} 1 \\ 0 \\ \end{array}\right ] = \left [ \begin{array}{c} 1/2 \\ 0 \\ \end{array}\right ]. $
Norme
La norme d’un vecteur ou d’une matrice $V$ est « une mesure de longueur » notée $\Vert V \Vert $ ayant les propriétés suivantes :
– La norme est toujours positive : $\Vert V \Vert \geq 0$.
– La norme est proportionnelle : $\Vert a V \Vert \geq \vert a \vert \Vert V \Vert$ lorsque $a$ est un scalaire.
– La norme respecte l’inégalité du triangle : $\Vert V + W \Vert \leq \Vert V \Vert + \Vert W \Vert$.
En termes plus simples, on peut exprimer ces conditions comme ceci :
– la longueur d’un vecteur ne peut être négative ;
– si on multiplie les composantes d’un vecteur par $a$, alors le vecteur est $a$ fois plus long ;
– si on dessine un triangle, alors la somme de deux des côtés d’un triangle doit être plus grande que l’autre côté.

Norme euclidienne et norme de Frobenius
La norme euclidienne est tout simplement la racine carrée de la somme des composantes au carré : $\Vert V \Vert = \sqrt{ \sum_i \vert V_i \vert^2}$. Étant donné un vecteur $V=(a,b)$, la norme est $\Vert V \Vert = \sqrt{a^2+b^2}$. À moins de mention contraire, nous utilisons toujours la norme euclidienne.
En Java, on peut calculer la norme euclidienne d’un vecteur comme ceci :
float[] v = new float[3];
v[0] = 1;
v[1] = 3;
v[2] = 5;
float norme = .0f;
for(int k = ; k < v.length; ++k) norme += v[k]*v[k];
return Math.sqrt(norme);Dans le cas d’une matrice, la norme euclidienne prend le nom de la norme de Frobenius :
$\Vert M \Vert = \sqrt{\sum_{i,j} \vert M_{i,j} \vert^2 }.$
Voici un exemple :
$\left \Vert \begin{array}{cc} 1 & 0\\ 1 & 1 \\ 3 & 2 \end{array}\right \Vert = \sqrt{1+1+1+3^2+2^2}=4. $
La norme de Frobenius est sous-multiplicative, c’est-à-dire que
$\Vert M P \Vert \leq \Vert M \Vert \Vert P \Vert$
et cette relation s’applique que $P$ soit une matrice ou un vecteur.
Produit scalaire
Le produit scalaire entre deux vecteurs est la somme du produit de leurs composantes une à une :
$V\cdot W = \sum_i V_i W_i$
Pour pouvoir calculer le produit scalaire de deux vecteurs, il faut qu’ils aient le même nombre de composantes.
Voici un exemple :
$\left [ \begin{array}{c} 1 \\ 1 \\ 3 \end{array}\right ] \cdot \left [ \begin{array}{c} 1 \\ 1 \\ 1 \end{array}\right] = 5. $
On peut calculer le produit scalaire en Java avec le code suivant :
float[] v = new float[3];
float[] w = new float[3];
v[0] = 1; w[0] = 1;
v[1] = 3; w[1] = 3;
v[2] = 5; w[2] = 2;
float produit = .0f;
assert v.length == w.length;
for(int k = ; k < v.length; ++k) produit += v[k]*w[k];Voici un script JavaScript qui calcule le produit scalaire :
V2:
On peut vérifier que $\Vert V \Vert^2 =V\cdot V$. De plus, le vecteur $\frac{V}{\Vert V \Vert}$ est unitaire, c’est-à-dire qu’il a une norme de 1 : $\Vert\frac{V}{\Vert V \Vert}\Vert=1$.
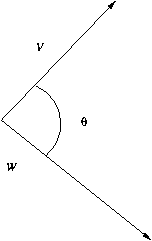
Le cosinus entre deux vecteurs est donné par :
$\cos \theta = \frac{V\cdot W}{\Vert V \Vert \Vert W \Vert}$.
Le script suivant calcule le cosinus entre deux vecteurs :
V2:
Vecteurs orthogonaux
Les vecteurs $V$, $W$ et $Z$ sont orthogonaux si le produit scalaire entre les vecteurs est nul : $V\cdot W = 0$, $V \cdot Z=0$ et $W \cdot Z = 0$. On dit qu’ils sont orthonormaux si en plus d’être orthogonaux, leur norme est unitaire : $\Vert V \Vert^2= V\cdot V = 1$, $\Vert W \Vert^2= W \cdot W=1$ et $\Vert Z \Vert^2=Z \cdot Z = 1$.
Par exemple, les vecteurs suivants sont orthogonaux :
$\left [ \begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right ] , \left [ \begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right] , \left [ \begin{array}{c} 0 \\ -1 \\ 1 \end{array}\right], $
alors que les vecteurs suivants sont orthonormaux :
$\left [ \begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right ] , \left [ \begin{array}{c} 0 \\ 1/\sqrt{2} \\ 1/\sqrt{2} \end{array}\right] , \left [ \begin{array}{c} 0 \\ -1/\sqrt{2} \\ 1/\sqrt{2} \end{array}\right]. $
Matrice diagonalisable
Une matrice carrée $M$ est diagonalisable s’il existe une matrice inversible $P$ telle que $P M P^{-1}$ est une matrice diagonale. Toutes les matrices normales sont diagonalisables, mais toutes les matrices ne sont pas diagonalisables. Les valeurs trouvées sur la diagonale sont appelées les valeurs propres de la matrice et sont toujours les mêmes, même si le choix de $P$ n’est pas toujours unique. Vous n’aurez pas à diagonaliser des matrices dans ce cours.
Un vecteur propre est un vecteur $x$ tel que $Mx = \lambda x$ où $\lambda$ est un scalaire appelé valeur propre.
Si $M$ est une matrice diagonalisable $n \times n$, alors il existe $n$ vecteurs propres orthogonaux dont les valeurs propres correspondent aux valeurs sur la diagonale de $P M P^{-1}$.
Note : une définition équivalente dit qu’une matrice carrée $M$ est diagonalisable s’il existe une matrice inversible $P$ telle que $P^{-1} M P$ est une matrice diagonale.
Métrique
Une métrique est une mesure de distance entre deux points satisfaisant les conditions suivantes :
- $d(x, y) \geq 0 $ (une distance ne peut être négative) ;
- $d(x,y) = 0$ si et seulement si $x=y$ (si la distance est nulle, c’est que les deux points sont au même endroit) ;
- $d(x,y) = d(y, x)$ (la distance de x à y est la même que la distance de y à x) ;
- $d(x, z) \leq d(x, y) + d(y,z)$ (inégalité du triangle).
Étant donné une norme, on peut définir une métrique comme suit $d(x,y)=\Vert x-y \Vert$.
Exemple 1. La distance euclidienne entre deux vecteurs $x,y$ est définie par le produit scalaire : $d(x,y)=\sqrt{ (x-y)\cdot (x-y) }$.
Exemple 2. L’angle entre deux vecteurs n’est pas une métrique.
Exemple 3. La distance de Hamming est un exemple de métrique. On définit la distance de Hamming entre deux chaînes de caractères de même longueur comme étant le nombre de caractères qui sont différents. Par exemple, la distance de Hamming entre « 123cb » et « 133cc » est 2.
Matrice orthonormale
Les colonnes d’une matrice peuvent être vues comme des vecteurs. Si l’ensemble de tous ces vecteurs sont orthonormaux, alors la matrice est orthonormale [2]. Une matrice orthonormale satisfait $M^tM=I$, c’est-à-dire
que sa transposée est son inverse par la droite. Une matrice orthonormale n’est pas nécessairement carrée.
Cette matrice est orthonormale :
$\left [ \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1/\sqrt{2} & -1/\sqrt{2} \\ 0 & 1/\sqrt{2} & 1/\sqrt{2} \end{array}\right ]. $
Attention de ne pas confondre les matrices orthonormales avec les matrices normales ! Par exemple, une matrice qui n’est pas carrée ne peut être normale, mais elle peut être orthonormale. La matrice suivante est normale, mais pas orthonormale :
$\left [ \begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right ]. $
Par contre, une matrice carrée orthonormale est nécessairement normale.
Décomposition en valeurs singulières
Toutes les matrices $M$ peuvent s’écrire sous la forme $M=USV^t$ où $U$ et $V$ sont orthonormales et $S$ est une matrice diagonale [3]. Vous n’aurez pas à calculer la décomposition en valeurs singulières d’une matrice dans ce cours ; il existe d’ailleurs des librairies logicielles bien au point pour le faire à votre place si le besoin se présente.
L’intérêt de la décomposition en valeurs singulières est de pouvoir manipuler une matrice diagonale au lieu de la matrice originale. Cette technique mathématique est à la base d’un modèle en recherche d’information appelé Latent Semantic Indexing.
On peut aussi utiliser la décomposition en valeurs singulières pour calculer la pseudo-inverse d’une matrice. En effet, si on a la décomposition $M=USV^t$ où $S$ est une matrice diagonale ayant les valeurs $\sigma_i$ sur la diagonale, alors la pseudo-inverse de $M$ est donnée par $US^*V^t$ où $S^*$ est la matrice diagonale ayant les valeurs $1/\sigma_i$ sur la diagonale avec la convention $1/0=0$.
Le cas des matrices déjà diagonales est très simple. La décomposition en valeurs singulières de la matrice
$\left [ \begin{array}{cc} 2 & 0 \\ 0 & 3 \\ \end{array}\right ]$
est tout simplement
$ \left [ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array}\right ] \left [ \begin{array}{cc} 2 & 0 \\ 0 & 3 \\ \end{array}\right ] \left [ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array}\right ] $
et la matrice pseudo-inverse est
$ \left [ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array}\right ] \left [ \begin{array}{cc} 1/2 & 0 \\ 0 & 1/3 \\ \end{array}\right ] \left [ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array}\right ]=\left [ \begin{array}{cc} 1/2 & 0 \\ 0 & 1/3 \\ \end{array}\right ]. $
JAMA
Il existe de nombreuses librairies, en Java et dans tous les autres langages, pour faire toutes les opérations que nous avons décrites sur les vecteurs et matrices. Certaines de ces opérations sont plus difficiles, comme l’inversion d’une matrice ou sa décomposition en valeurs singulières. La librairie Java « JAMA » est une librairie du domaine public qui permet de faire ces opérations et plusieurs autres. Vous pouvez librement l’utiliser dans vos programmes Java.
Références
– Les articles matrice et vecteur dans l’encyclopédie Wikipédia contiennent de l’information et des exemples supplémentaires.
– Les étudiants qui ont besoin d’une référence peuvent acquérir le volume de Luc Amyotte sur l’introduction à l’algèbre linéaire.
[1] On peut toujours vérifier facilement si une matrice est normale en faisant la multiplication des matrices.
[2] Certains auteurs appellent de telles matrices des matrices
orthogonales, mais d’autres réservent cette appellation aux matrices carrées. D’autres auteurs, encore, exigent que les rangées de la matrice, plutôt que les colonnes, soient des vecteurs orthogonaux.
[3] L’énoncé exact de la définition peut varier d’un auteur à l’autre, mais toutes les définitions devraient être équivalentes.




