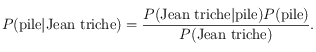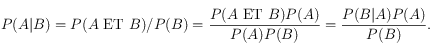Probabilités |
 |
Présentation et motivation
On peut ne pas voir immédiatement le lien entre les probabilités et la recherche d’information, mais ce lien deviendra rapidement très clair au fur et à mesure que le cours progressera. Les probabilités sont utilisées tant dans les modèles de la langue, que dans les algorithmes de Google (PageRank) ou dans les moteurs de recherche. En somme, elles sont incontournables.
Si vous n’avez pas étudié les probabilités auparavant, ce texte peut vous paraître difficile ou déroutant. N’ayez crainte. Vous aurez la possibilité de revenir sur ces notions en tout temps dans le cours et vous pourrez vérifier le degré de votre compréhension dans l’activité d’autoévaluation.
La moyenne
La moyenne d’un vecteur ![]() est la somme de ses composantes divisée par le nombre de composantes ; elle est notée
est la somme de ses composantes divisée par le nombre de composantes ; elle est notée ![]() . La formule est
. La formule est 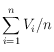 .
.
La variance
La variance d’un vecteur ![]() est la somme du carré de l’écart à la moyenne des composantes divisée par le nombre de composantes. La formule est la suivante :
est la somme du carré de l’écart à la moyenne des composantes divisée par le nombre de composantes. La formule est la suivante : 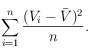
Voici un script JavaScript qui calcule la moyenne et la variance d’un vecteur :
(Le script ne fonctionne pas dans tous les navigateurs.)
La corrélation
Étant donné deux vecteurs de même taille, on peut calculer la corrélation de Pearson entre les deux vecteurs comme étant :
La corrélation de Pearson est une valeur entre -1 et 1. Le carré de la corrélation de Pearson donne le pourcentage de corrélation.
Par exemple, ces deux vecteurs sont fortement corrélés (corrélation proche de 1) :
alors que ces deux vecteurs sont aussi fortement corrélés, mais négativement (corrélation de -1) :
Finalement, il n’y a aucune corrélation entre ces deux vecteurs (corrélation de 0) :
La fréquence
La fréquence est le nombre de fois qu’une instance ou qu’un objet se manifeste. Par exemple, la fréquence du mot rue dans le journal est le nombre de fois que le mot rue est utilisé dans les textes du journal.
La distribution
Dans le cadre de ce cours, une distribution est une fonction qui, pour chaque instance possible, nous donne la probabilité correspondante. La somme de toutes les probabilités doit être 1.
La distribution des probabilités du lancer d’une pièce de monnaie est 50% pour l’instance pile et 50% pour l’instance face.
Si on choisit un mot au hasard dans un texte, quelle est la probabilité que le mot soit rue ou voiture ? Dans ce cas, on peut calculer la distribution avec exactitude si on connaît d’avance le texte : il suffit de calculer la fréquence de chaque mot et de la diviser par le nombre total de mots.
La moyenne et la variance d’une distribution
Notons ![]() la probabilité que la valeur d’une certaine variable soit
la probabilité que la valeur d’une certaine variable soit ![]() . Par exemple, si on attribue la valeur 1 au résultat pile et la valeur 0 au résultat face, alors la distribution d’un lancer d’une pièce de monnaie est
. Par exemple, si on attribue la valeur 1 au résultat pile et la valeur 0 au résultat face, alors la distribution d’un lancer d’une pièce de monnaie est ![]() et
et ![]() . Notez que
. Notez que ![]() .
.
La moyenne ou l’espérance d’une distribution est :
alors que sa variance est :
Voici un script JavaScript qui calcule la moyenne et la variance d’un vecteur :
P(k=2) =
P(k=3) =
La distribution de Poisson
Dans une distribution de Poisson, la probabilité pour qu’une valeur donnée soit ![]() , est
, est
où ![]() est un paramètre et
est un paramètre et ![]() . La variance et la moyenne d’une distribution de Poisson est
. La variance et la moyenne d’une distribution de Poisson est ![]() .
.
Le rang
Étant donné une distribution, l’instance la plus probable occupe le premier rang, la deuxième instance la plus probable occupe le second rang et ainsi de suite.
Par exemple, dans le problème qui consiste à choisir au hasard un mot dans un texte, le mot le plus fréquent aura le premier rang et le mot le moins fréquent, le dernier rang.
La probabilité
La probabilité est toujours une valeur entre 0 (un événement impossible) et 1 (un événement certain). En général, on note la probabilité que l’événement ![]() se produise
se produise ![]() et la probabilité qu’il ne se produise pas
et la probabilité qu’il ne se produise pas ![]() . Nous savons que
. Nous savons que ![]() .
.
Si on est certain qu’un (et un seul) des événements ![]() ,
, ![]() ou
ou ![]() doit se produire, nous avons
doit se produire, nous avons ![]() .
.
![]() est la probabilité que
est la probabilité que ![]() et
et ![]() se produisent.
se produisent.
Les événements ![]() et
et ![]() sont indépendants si et seulement si
sont indépendants si et seulement si ![]() .
.
Les divers lancers d’une pièce de monnaie sont indépendants et donc, la probabilité d’obtenir deux fois pile est ![]() (25%).
(25%).
Note. Certains auteurs utilisent le et et le ou logiques : ![]() et
et ![]() . Personnellement, je trouve qu’il est difficile de se rappeler lequel de
. Personnellement, je trouve qu’il est difficile de se rappeler lequel de ![]() et de
et de ![]() signifie « et » et lequel signifie « ou ». Dans ce cours, nous n’utiliserons pas cette notation.
signifie « et » et lequel signifie « ou ». Dans ce cours, nous n’utiliserons pas cette notation.
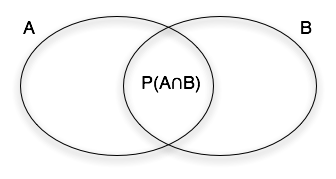
La probabilité conditionnelle et la vraisemblance
La probabilité qu’au lancer d’une pièce de monnaie, on obtienne pile peut être notée ![]() . Nous avons, bien sûr,
. Nous avons, bien sûr, ![]() . La probabilité conditionnelle est la probabilité attribuée à un fait connu. Par exemple, si on sait que Jean triche, on pourra avoir une probabilité différente, disons de 60% pour la valeur pile. On note la probabilité conditionnelle avec la barre verticale, comme ceci :
. La probabilité conditionnelle est la probabilité attribuée à un fait connu. Par exemple, si on sait que Jean triche, on pourra avoir une probabilité différente, disons de 60% pour la valeur pile. On note la probabilité conditionnelle avec la barre verticale, comme ceci : ![]() .
.
Formellement, on définit la probabilité conditionnelle (![]() ) comme
) comme
![]() . Ainsi, si la probabilité que Jean triche est de 5% et qu’il arrive dans 3% des cas que Jean ait triché et que le résultat soit pile, on dira que la probabilité conditionnelle d’avoir pile étant donné que Jean triche est de 60%. Nous avons
. Ainsi, si la probabilité que Jean triche est de 5% et qu’il arrive dans 3% des cas que Jean ait triché et que le résultat soit pile, on dira que la probabilité conditionnelle d’avoir pile étant donné que Jean triche est de 60%. Nous avons ![]() . En général,
. En général, ![]() ; cependant, on peut calculer l’une des valeurs à partir de l’autre en utilisant le théorème de Bayes.
; cependant, on peut calculer l’une des valeurs à partir de l’autre en utilisant le théorème de Bayes.
Le théorème de Bayes stipule que 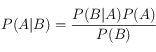 où, dans le cas de notre exemple,
où, dans le cas de notre exemple,
Il n’est pas nécessaire de mémoriser ce théorème dans ce cours, mais il faut savoir que c’est le principal théorème utilisé avec les probabilités conditionnelles. Il est facile de le démontrer à partir de la définition ![]() :
:
La vraisemblance est définie comme ![]() . Ainsi, la vraisemblance que Jean triche étant donné un résultat pile est 60% (
. Ainsi, la vraisemblance que Jean triche étant donné un résultat pile est 60% (![]() ), si on suppose que personne d’autre ne triche, et que pile et face sont équiprobables, alors la vraisemblance que Jean ne triche pas étant donné un résultat pile est de 50%. Contrairement à ce qui se passe avec les probabilités, les vraisemblances d’événements mutuellement exclusifs ne totalisent pas 100%.
), si on suppose que personne d’autre ne triche, et que pile et face sont équiprobables, alors la vraisemblance que Jean ne triche pas étant donné un résultat pile est de 50%. Contrairement à ce qui se passe avec les probabilités, les vraisemblances d’événements mutuellement exclusifs ne totalisent pas 100%.
Estimation des probabilités par vraisemblance maximale
Nous n’avons pas toujours accès à toutes les données lorsqu’il faut calculer les probabilités et nous sommes souvent forcés de les estimer. La façon la plus simple d’estimer les probabilités consiste à recourir à la méthode de vraisemblance maximale.
Supposons que vous preniez des échantillons de fleurs dans un parc. Sur 50 fleurs que vous avez ramassées, 12 fleurs sont des pissenlits et le reste, des trèfles blancs. Quelle est le probabilité que la prochaine fleur que vous ramassiez soit un pissenlit ? Une réponse fort naturelle est 12/50. C’est en effet la réponse la plus vraisemblable étant donné notre échantillonnage. Ainsi, si nous avons ![]() échantillons et que nous observons l’élément
échantillons et que nous observons l’élément ![]() ,
, ![]() fois, alors la probabilité associée à
fois, alors la probabilité associée à ![]() sera
sera ![]() .
.
Dans le cours, nous verrons que ce n’est pas seule méthode utilisée pour estimer des probabilités. Le lissage de Laplace et la formule de Good-Turing sont d’autres méthodes souvent utilisées.
La probabilité : toute une discipline
Il y aurait encore beaucoup à écrire sur les probabilités. Il faudrait traiter des équations de Chernoff, de Chebyshev, etc. Cependant, dans le cadre de ce cours, bien comprendre les notions présentées ici sera suffisant.
Lectures complémentaires fortement suggérées
– Une introduction improbable aux probabilités (chaudement recommandé, à consulter absolument !)
– Article de Wikipédia sur les probabilités (excellent !)



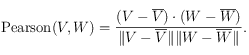
![V= \left [ \begin{array}{c}
1 \\
2 \\
3
\end{array}\right ], W= \left [ \begin{array}{c}
1.1 \\
2 \\
3.2
\end{array}\right ] V= \left [ \begin{array}{c}
1 \\
2 \\
3
\end{array}\right ], W= \left [ \begin{array}{c}
1.1 \\
2 \\
3.2
\end{array}\right ]](local/cache-TeX/86a4b8427b00cc93e262264239ac41c4.png)
![V= \left [ \begin{array}{c}
1 \\
2 \\
-3
\end{array}\right ], W= \left [ \begin{array}{c}
-1 \\
-2 \\
3
\end{array}\right ]. V= \left [ \begin{array}{c}
1 \\
2 \\
-3
\end{array}\right ], W= \left [ \begin{array}{c}
-1 \\
-2 \\
3
\end{array}\right ].](local/cache-TeX/27c42cfdd912c18f8432eb0201950059.png)
![V= \left [ \begin{array}{c}
1 \\
2 \\
-3
\end{array}\right ] , W= \left [ \begin{array}{c}
-2 \\
1 \\
0
\end{array}\right ]. V= \left [ \begin{array}{c}
1 \\
2 \\
-3
\end{array}\right ] , W= \left [ \begin{array}{c}
-2 \\
1 \\
0
\end{array}\right ].](local/cache-TeX/3e4d6aafbe26f900ec93629a377738f2.png)