Autoévaluation |
 |
Rappel. Il est essentiel dans ce cours de faire toutes les activités d’autoévaluation pour vous préparer à l’examen final et aux travaux notés. Pour chaque question, tentez d’abord, honnêtement, de trouver la réponse, puis vérifiez la solution. En cas de doute, retournez lire les textes de la semaine.
Question 1
Quel est le résultat de cette multiplication :
![\left [ \begin{array}{ll}
1 & 2 \\
3 & 4
\end{array} \right ]
\left [ \begin{array}{l}
1 \\
3
\end{array} \right ] \left [ \begin{array}{ll}
1 & 2 \\
3 & 4
\end{array} \right ]
\left [ \begin{array}{l}
1 \\
3
\end{array} \right ]](local/cache-TeX/2350dd712cc7755516a0c20b0b5420b2.png) ?
?
Question 2
Si je multiplie une matrice ![]() avec un vecteur et que le temps de calcul est de 0.1 s, quel sera (approximativement) le temps de calcul si je multiplie une matrice
avec un vecteur et que le temps de calcul est de 0.1 s, quel sera (approximativement) le temps de calcul si je multiplie une matrice ![]() avec un vecteur ?
avec un vecteur ?
Question 3
Quelle est la norme euclidienne de cette matrice :
![\left [ \begin{array}{ll}
1 & 2 \\
3 & 4
\end{array} \right ] \left [ \begin{array}{ll}
1 & 2 \\
3 & 4
\end{array} \right ]](local/cache-TeX/60b34bceb93dca0a6a23970a31f0e484.png) ?
?
Question 4
Quelle est la corrélation de Pearson entre ces deux vecteurs :
![V= \left [ \begin{array}{c}
1 \\
2 \\
3
\end{array}\right ], W= \left [ \begin{array}{c}
1.1 \\
2 \\
2.9
\end{array}\right ] V= \left [ \begin{array}{c}
1 \\
2 \\
3
\end{array}\right ], W= \left [ \begin{array}{c}
1.1 \\
2 \\
2.9
\end{array}\right ]](local/cache-TeX/a5825aae1daa978bb3bb429b55832e03.png) ?
?
Question 5
Quel est le cosinus de ces deux vecteurs :
![V= \left [ \begin{array}{c}
1 \\
0 \\
0
\end{array}\right ], W= \left [ \begin{array}{c}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} \\
0
\end{array}\right ] V= \left [ \begin{array}{c}
1 \\
0 \\
0
\end{array}\right ], W= \left [ \begin{array}{c}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} \\
0
\end{array}\right ]](local/cache-TeX/85e7a4eeb050ce94315194e0d9f17151.png) ?
?
Question 6
Pourquoi est-ce que la matrice suivante est diagonalisable ?
Question 7
En quel temps s’exécute un algorithme qui, étant donné un mot, le cherche dans 1000 documents en faisant une recherche « mot à mot » dans chaque document ?
Question 8
Est-ce que la multiplication de matrices carrées selon l’algorithme proposé dans ce cours est une opération en temps quadratique ![]() ou en temps linéaire
ou en temps linéaire ![]() ?
?
Question 9
Supposons qu’une matrice diagonalisable ![]() ait toutes ses valeurs propres entre 0 et
ait toutes ses valeurs propres entre 0 et ![]() . Étant donné un vecteur arbitraire
. Étant donné un vecteur arbitraire ![]() , que pouvez-vous dire sur
, que pouvez-vous dire sur ![]() ?
?
Question 10
Soit ![]() trois vecteurs, si
trois vecteurs, si ![]() et
et ![]() , qu’est-ce que
, qu’est-ce que ![]() ?
?
Question 11
Montrez que ![]() .
.
Question 12
Quelle est la distribution des probabilités d’un lancer de deux dés où l’on fait la somme des deux dés ? À partir de la distribution, calculez la moyenne.
Question 13
En supposant que les lancers d’un dé sont des événements indépendants, quelle est la probabilité d’obtenir un 6 au premier lancer, sans obtenir encore un 6 au second lancer ?
Question 14
Vous lancez un dé deux fois. Quelle est la probabilité d’obtenir 2 fois 6 au cours de deux lancers de dé si vous avez obtenu un 6 au premier lancer ? Présentez le calcul sous la forme d’une formule.
Question 15
Calculez une décomposition en valeurs singulières de la matrice :
Question 16
Calculez la pseudo-inverse de :
Question 17
Jean est jardinier et sait que dans un certain quartier, le nombre de fleurs par jardin suit une loi de Poisson. La moyenne du nombre de fleurs dans un jardin est 10. Quelle est la probabilité qu’un jardin n’ait aucune fleur ?
Question 18
Soit le vecteur ![]() . Quelle est la moyenne et la variance des valeurs qu’il contient ?
. Quelle est la moyenne et la variance des valeurs qu’il contient ?
Question 19
Soit la distribution ![]() ; quelles sont la moyenne et la variance de cette distribution ? Quelle est l’espérance de la distribution ?
; quelles sont la moyenne et la variance de cette distribution ? Quelle est l’espérance de la distribution ?
Question 20
Si la distribution ![]() a été calculée par vraisemblance maximale et que la valeur 1 s’est produite 200 fois, combien d’événements au total aurons-nous observés ?
a été calculée par vraisemblance maximale et que la valeur 1 s’est produite 200 fois, combien d’événements au total aurons-nous observés ?
Question 21
Si ![]() est une distribution de Poisson, montrez que
est une distribution de Poisson, montrez que ![]()
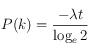 +
+ ![]() -
- ![]()
![]() .
.
Question 22
Trois chaînes de caractères sont de même longueur : la distance de Hamming entre la première chaîne et la deuxième chaîne est de 1, et la distance de Hamming entre la deuxième et la troisième chaîne est de 2 ; que pouvez-vous dire sur la distance de Hamming entre la première et la dernière chaîne ?
Question 23
Une matrice diagonalisable ![]() a les valeurs propres 1, 2 et 3. Quelles sont les valeurs propres de
a les valeurs propres 1, 2 et 3. Quelles sont les valeurs propres de ![]() ?
?
Question 24
Si j’ai un risque sur 3 d’avoir un accident de voiture, une chance sur deux de tomber en amour, et un risque sur 4 d’avoir un accident si je suis tombé en amour, quelle est la probabilité que je tombe en amour étant donné que j’ai eu un accident ?
Question 25
Expliquez le lien entre la fréquence d’occurence et la probabilité. Est-ce la même chose ?
Question 26
En Ontario, selon Radio-Canada, les détaillants de billets ont remporté 214 lots importants au cours des sept années entre 1998 et 2005. Supposons qu’il y ait 150 détaillants de loterie en Ontario et que chaque détaillant achète dix billets par semaine. Supposons, de plus, que la probabilité de gagner un lot important soit de un sur 1 million. Quel est le nombre attendu de lots importants gagnés par des détaillants ?
Question 27
Vous participez à un jeu télévisé. On vous demande de choisir entre trois portes. Derrière l’une des portes se trouve le grand prix. Vous choisissez l’une des portes, au hasard, sans l’ouvrir. Le présentateur, lui, ouvre alors une seconde porte derrière laquelle ne se trouve pas le grand prix. Il reste donc deux portes fermées : celle que vous avez choisie et la porte restante. Il vous donne alors le choix entre conserver votre porte actuelle ou opter pour ouvrir la porte restante. Que faites-vous ?
Question 28
Un pour cent des femmes ayant plus de quarante ans et participant à un test de dépistage ont le cancer du sein.
Environ 80 % des femmes ayant le cancer du sein obtiennent un test de mammographie positif.
Seulement 9.6 % des femmes n’ayant pas le cancer du sein obtiennent un test de mammographie positif.
Une femme de plus de quarante ans a passé un test de mammographie qui s’est avéré positif. Quelle est la probabilité qu’elle ait le cancer ?
Question 29
Dans un éditorial de la revue Webology (Volume 5, Number 4, December, 2008), Alireza Noruzi fait la constatation suivante :
(...) only a small fraction of the top 100 papers ranked by the number of citations (17 of 100) were published by single authors.
De cette constation, Noruzi en tire la conclusion suivante :
(...) a published paper resulting from collaborative work has a higher chance of attracting more citations.
Que pensez-vous de cette analyse ?
Question 30
Prouvez que ![]() .
.
Question 31
Qu’est-ce que 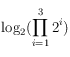 ? (Sans calculatrice ou ordinateur.)
? (Sans calculatrice ou ordinateur.)
Question 32
Qu’est-ce que ![]() ? (Sans calculatrice ou ordinateur.)
? (Sans calculatrice ou ordinateur.)



![V-\overline{V}= \left [ \begin{array}{c}
-1 \\
0 \\
1
\end{array}\right ], W-\overline{W}= \left [ \begin{array}{c}
-0.9 \\
0 \\
0.9
\end{array}\right ] V-\overline{V}= \left [ \begin{array}{c}
-1 \\
0 \\
1
\end{array}\right ], W-\overline{W}= \left [ \begin{array}{c}
-0.9 \\
0 \\
0.9
\end{array}\right ]](local/cache-TeX/62f45b3dbf88374df4a585a3a0142296.png) .
.![\left [ \begin{array}{ccc}
1 & 2 & 0 \\
2 & 4 & 1\\
0 & 1 & 1
\end{array}\right ] \left [ \begin{array}{ccc}
1 & 2 & 0 \\
2 & 4 & 1\\
0 & 1 & 1
\end{array}\right ]](local/cache-TeX/56ccaf04c242545ffa8a4a848c148308.png)
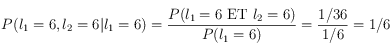 .
.
![\left [ \begin{array}{ll}
1 & 0 \\
0 & 2 \\
0 & 0
\end{array} \right ]. \left [ \begin{array}{ll}
1 & 0 \\
0 & 2 \\
0 & 0
\end{array} \right ].](local/cache-TeX/ade80701581fe916a1f2b5d70211032e.png)
![\left [ \begin{array}{ll}
1 & 0 \\
0 & 1 \\
0 & 0
\end{array} \right ]
\left [ \begin{array}{ll}
1 & 0 \\
0 & 2
\end{array} \right ]
\left [ \begin{array}{ll}
1 & 0 \\
0 & 1
\end{array} \right ].
\left [ \begin{array}{ll}
1 & 0 \\
0 & 1 \\
0 & 0
\end{array} \right ]
\left [ \begin{array}{ll}
1 & 0 \\
0 & 2
\end{array} \right ]
\left [ \begin{array}{ll}
1 & 0 \\
0 & 1
\end{array} \right ].](local/cache-TeX/9be44cbc03579a50f984e2440843147d.png)
![\left [ \begin{array}{ll}
3 & 0 \\
0 & 2 \\
0 & 0
\end{array} \right ]. \left [ \begin{array}{ll}
3 & 0 \\
0 & 2 \\
0 & 0
\end{array} \right ].](local/cache-TeX/cfe491a5f5af84c3efb6ac99b6007eaf.png)
![\left [ \begin{array}{ll}
1 & 0 \\
0 & 1 \\
0 & 0
\end{array} \right ]
\left [ \begin{array}{ll}
3 & 0 \\
0 & 2
\end{array} \right ]
\left [ \begin{array}{ll}
1 & 0 \\
0 & 1
\end{array} \right ]
\left [ \begin{array}{ll}
1 & 0 \\
0 & 1 \\
0 & 0
\end{array} \right ]
\left [ \begin{array}{ll}
3 & 0 \\
0 & 2
\end{array} \right ]
\left [ \begin{array}{ll}
1 & 0 \\
0 & 1
\end{array} \right ]](local/cache-TeX/3c742bf1657d89451a35e5a0983a6ac7.png)
![\left [ \begin{array}{ll}
1 & 0 \\
0 & 1 \\
0 & 0
\end{array} \right ]
\left [ \begin{array}{ll}
1/3 & 0 \\
0 & 1/2
\end{array} \right ]
\left [ \begin{array}{ll}
1 & 0 \\
0 & 1
\end{array} \right ]=
\left [ \begin{array}{ll}
1/3 & 0 \\
0 & 1/2 \\
0 & 0
\end{array} \right ].
\left [ \begin{array}{ll}
1 & 0 \\
0 & 1 \\
0 & 0
\end{array} \right ]
\left [ \begin{array}{ll}
1/3 & 0 \\
0 & 1/2
\end{array} \right ]
\left [ \begin{array}{ll}
1 & 0 \\
0 & 1
\end{array} \right ]=
\left [ \begin{array}{ll}
1/3 & 0 \\
0 & 1/2 \\
0 & 0
\end{array} \right ].](local/cache-TeX/6c6e2e49674991318f922c436870a8dd.png)
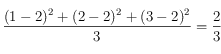 .
.
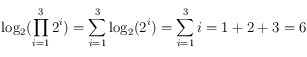 .
.
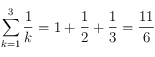 .
.

