Algorithme PageRank |
 |
Présentation
Le web peut être vu comme un graphe dirigé ![]() où les
où les
sommets ![]() sont les pages web [1] et les arcs
sont les pages web [1] et les arcs ![]() sont les hyperliens
sont les hyperliens
entre les pages. Les arcs partent de la page où se trouve le lien et vont vers la page indiquée.
Voici un exemple :
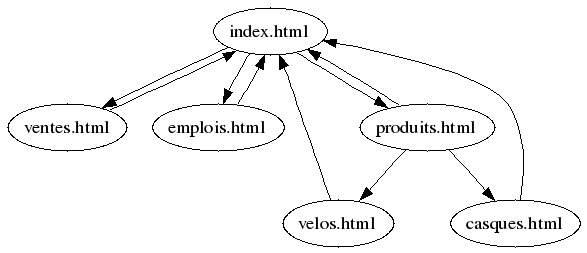
L’intuition qui se cache derrière l’algorithme PageRank [2]
est que la présence d’un lien vers une certaine page constitue un « vote » en faveur de cette page. En effet, en général, on place un lien vers une page parce qu’on la trouve intéressante. Basé sur la structure des liens, le « PageRank » est une mesure de l’importance relative d’une page sur le web. On peut obtenir la valeur PageRank de toute page sur le web à l’adresse : http://www.mygooglepagerank.com/.
La valeur PageRank est basée sur les principes suivants :
- Les pages recevant plus de liens sont sans doute plus importantes. En d’autres termes, PageRank est un système « pragmatique » : les pages sont jugées plus importantes si elles sont plus « populaires ».
- Un lien en provenance d’une page « importante » est plus significatif qu’un lien en provenance d’une page peu importante. En d’autres termes, si un lien vers une page est un « vote », certains votes comptent plus que d’autres !
- Si une page contient beaucoup de liens, chaque lien a moins de valeur.
On constate donc que l’importance d’une page est définie de façon circulaire : on définit l’importance des pages en présumant qu’on connaît déjà l’importance des pages ! Ce n’est pas pour autant une contradiction.
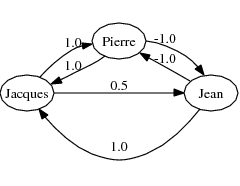
Voici un exemple de problème circulaire qui a pourtant une solution bien intéressante :
Exemple. Jean, Pierre et Jacques ont chacun une certaine quantité d’argent en banque. Jean avait autant d’argent que Jacques, mais il a donné une partie de ce qu’il avait à Pierre qui n’avait rien. Pierre a autant d’argent que Jacques si on soustrait ce que Jean a. Jacques a autant d’argent que la moitié de ce que Jean a, plus tout ce qu’a Pierre. S’ils ont au total 6 dollars, combien possède chaque compère ?
PageRank : l’arme « secrète » de Google
On a vu qu’étant donné tous les documents correspondant à une requête, on pouvait les classer par ordre de pertinence selon un modèle vectoriel (tel que tf.idf) ou probabiliste.
Cette même approche échoue dans un contexte aussi distribué que le web. On ne peut plus ne prendre en compte que le contenu du document pour en déterminer la pertinence. Il suffit de penser qu’avec un modèle vectoriel, et sachant d’avance quelles requêtes les gens préfèrent (« Harry Potter », « sexe », etc.), il serait facile de créer des documents sur mesure pour s’assurer d’avoir la meilleure mesure de pertinence.
L’algorithme PageRank que nous allons étudier est utilisé par Google pour « filtrer » et « classer » les pages. (Voir http://www.google.com/corporate/tec...) Pour l’essentiel, Google attribue un « PageRank » (mesure de popularité) à chaque page. Cette mesure est absolue (elle ne dépend pas des termes recherchés). De toutes les pages qui contiennent les termes recherchés, et en tenant compte d’autres facteurs [3], Google choisit quelles pages seront présentées en premier.
PageRank : version simplifiée
Comment définit-on PageRank mathématiquement ?
Étant donné une page web ![]() , si
, si ![]() est la liste
est la liste
des pages web pointant vers ![]() et
et ![]() est la liste
est la liste
des pages web vers lesquelles ![]() pointe, alors le facteur PageRank, noté
pointe, alors le facteur PageRank, noté ![]() ,
,
est 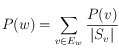
avec la convention que ![]() est la cardinalité de l’ensemble
est la cardinalité de l’ensemble ![]() . On peut lire cette formule comme suit : chaque page qui pointe vers
. On peut lire cette formule comme suit : chaque page qui pointe vers ![]() contribue à une fraction de sa propre réputation. Dans ce modèle,
contribue à une fraction de sa propre réputation. Dans ce modèle,
on suppose qu’une page ne peut faire de lien vers elle-même.
Une façon intuitive de décrire cette formule est d’imaginer un surfeur qui se promène de page en page, en partant au hasard sur une des pages. Lorsqu’il arrive à la page ![]() , il choisit au hasard (avec une probabilité
, il choisit au hasard (avec une probabilité
![]() l’un des liens et poursuit son chemin. Le facteur PageRank mesure avec quelle probabilité on retrouve le surfeur sur une page donnée, après qu’il ait suivi un très grand nombre de liens. Il s’agit bien sûr d’une chaîne de Markov.
l’un des liens et poursuit son chemin. Le facteur PageRank mesure avec quelle probabilité on retrouve le surfeur sur une page donnée, après qu’il ait suivi un très grand nombre de liens. Il s’agit bien sûr d’une chaîne de Markov.
Dans cet esprit, si une page ne contient aucun lien, on suppose au contraire qu’elle contient des liens
vers toutes les pages. En effet, on suppose que le surfeur, arrivé à une impasse, reprend son trajet à partir
d’une nouvelle page choisie au hasard. Cela nous assure que s’il y a au moins une telle page, la matrice de transition sera ergodique.
Ce modèle satisfait bien nos objectifs.
- Plus une page reçoit de liens, plus sa valeur
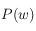 sera élevée : chaque lien ajoute un peu de poids au facteur PageRank.
sera élevée : chaque lien ajoute un peu de poids au facteur PageRank. - Plus une page est elle-même importante (valeur élevée de
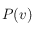 ), plus elle contribue au facteur PageRank des pages « récipiendaires » de liens.
), plus elle contribue au facteur PageRank des pages « récipiendaires » de liens. - Plus une page contient de liens, moins chaque lien contribue au facteur PageRank des pages « récipiendaires ».
Reprenons notre exemple avec les pages index.html, produits.html, etc. :
– index.html pointe vers 3 pages (ventes.html, emplois.html, produits.html) ;
– produits.html pointe vers 3 pages (velos.html, casques.html, index.html) ;
– emplois.html pointe vers une page (index.html) ;
– ventes.html pointe vers une page (index.html) ;
– velos.html pointe vers une page (index.html) ;
– casques.html pointe vers une page (index.html).
Pour simplifier la notation, nous écrivons ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() et
et
![]() .
.
On peut donc représenter la forme de calcul de PageRank à l’aide de la multiplication matricielle suivante
où la matrice est une matrice de « transition » parce que chaque rangée donne les probabilités de passage
à une autre état :
On peut lire cette matrice ainsi : une fois dans l’état « 1 » (page « index.html »), on a une chance sur 3 de passer aux états « 2 », « 3 » ou « 4 » (pages « produits.html », « emplois.html » et « ventes.html »).
D’un autre côté, si on est dans l’état « 3 », « 4 », « 5 » ou « 6 », on doit passer (avec une probabilité de 1)
à l’état « 1 » (page « index.html »). Notez que la somme des valeurs dans chaque rangée doit être obligatoirement 1. Il ne s’agit pas d’une matrice
de transition régulière : elle est ergodique.
La représentation du problème, sous une forme matricielle, implique que le vecteur recherché
est un vecteur propre de la matrice avec comme valeur propre la valeur unitaire (1).
Comment peut-on calculer le vecteur ![]() ? C’est en fait très simple. Il suffit de partir de n’importe quel vecteur de probabilité (vecteur dont la somme des composantes est 1 [4]) et d’appliquer à répétition la matrice de transition. On peut choisir comme vecteur
? C’est en fait très simple. Il suffit de partir de n’importe quel vecteur de probabilité (vecteur dont la somme des composantes est 1 [4]) et d’appliquer à répétition la matrice de transition. On peut choisir comme vecteur
de probabilité une distribution uniforme (![]() ). Parce qu’il s’agit
). Parce qu’il s’agit
d’une chaîne de Markov ergodique [5], on sait qu’elle convergera éventuellement vers un vecteur qui représentera alors le PageRank.
Points importants :
– L’application à répétition de la matrice de transition à un vecteur converge (peu importe le vecteur choisi). Cependant, la vitesse de convergence peut être très lente.
– Ce calcul converge vers la même valeur peu importe le vecteur initial choisi.
Il est intéressant de noter qu’on peut calculer les puissances d’une matrice (ou de n’importe quelle quantité) de façon efficace : si ![]() est notre matrice, on peut d’abord calculer
est notre matrice, on peut d’abord calculer ![]() , puis
, puis ![]() , puis
, puis ![]() , puis
, puis ![]() . En d’autres mots, on peut calculer la puissance
. En d’autres mots, on peut calculer la puissance ![]() d’une matrice en ne faisant que
d’une matrice en ne faisant que ![]() multiplications ! C’est drôlement plus efficace, surtout si la matrice est importante !
multiplications ! C’est drôlement plus efficace, surtout si la matrice est importante !
Rappelons que la multiplication d’une matrice n par n se fait en temps ![]() [6] Naturellement, si la matrice contient plusieurs zéros on peut ainsi gagner encore plus de temps, ce qui sera le cas pour la matrice du web parce que la plupart des pages n’ont de liens que vers très peu de pages.
[6] Naturellement, si la matrice contient plusieurs zéros on peut ainsi gagner encore plus de temps, ce qui sera le cas pour la matrice du web parce que la plupart des pages n’ont de liens que vers très peu de pages.
PageRank : version non simplifiée
Un problème auquel fait face la version simplifiée de l’algorithme PageRank est que si une partie du web, par exemple un réseau d’amis ayant des sites web, fait un lien vers le reste du web, mais que personne ailleurs dans le web ne fait un lien vers eux, alors le PageRank de ce sous-réseau sera nul !
Prenons l’exemple de cette matrice de transition :
On voit que l’état « 2 » et l’état « 4 » ne reçoivent aucun « lien » des états « 1 » et « 3 » : une fois notre surfeur sur les pages « 1 » et « 3 », il ne peut revenir ! Par contre, on peut passer de la page « 2 », à la page « 1 » ou à la page « 3 ».
On voit que les pages « 2 » et « 4 » reçoivent un PageRank de zéro si on fait le calcul suivant :
Afin de limiter cet effet, on suppose que le surfeur aléatoire, après
avoir suivi quelques hyperliens, recommencera à zéro. On lui accorde donc, à l’arrivée sur une page, une petite probabilité de quitter la page courante pour reprendre une page au hasard. Cela vient éliminer, en grande partie, l’effet déplorable que nous venons de décrire.
Si ![]() est un coefficient de calibrage (
est un coefficient de calibrage (![]() ) et
) et ![]() est le
est le
nombre total de pages web, alors la version complète de PageRank prend la forme suivante :
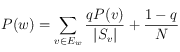
On attribue une probabilité de 15 % au fait que le surfeur ne suive pas les liens et reprenne son cybersurf du début. Le facteur ![]() sert à « compenser pour » le coefficient
sert à « compenser pour » le coefficient ![]() ajouté à la fraction
ajouté à la fraction ![]() , de manière à ce que la somme des probabilités demeure 1 : si on perd 15 % de probabilités, il faut regagner ce pourcentage ailleurs.
, de manière à ce que la somme des probabilités demeure 1 : si on perd 15 % de probabilités, il faut regagner ce pourcentage ailleurs.
Si on applique ce facteur à notre exemple (représenté sur le premier graphe en haut de la page), nous obtenons la matrice de transition suivante :
Le calcul du PageRank se fait comme avec l’algorithme PageRank simplifié. Un des avantages d’utiliser un paramètre ![]() est qu’une valeur plus petite de
est qu’une valeur plus petite de ![]() accélère la convergence ; la valeur
accélère la convergence ; la valeur ![]() assure une bonne convergence en pratique.
assure une bonne convergence en pratique.
La normalisation du PageRank
Le calcul du PageRank tel qu’on le fait ici est normalisé de telle manière que la somme des valeurs pour chaque page donnera « 1 ». Si nous avons 8 milliards de pages web, nous obtiendrons alors que la valeur moyenne du PageRank pour une page donnée est 1/8 milliard, ce qui est un très petit nombre. Dans l’article original, Brin et Page proposaient une valeur moyenne du PageRank de 1.0. On constate maintenant sur http://www.mygooglepagerank.com/ que la valeur du PageRank se situe entre 0 et 10. On pense aussi qu’il s’agit d’une échelle logarithmique. Ainsi, Google normalise la valeur du PageRank.
Utilisation de PageRank dans un moteur de recherche
Tel que nous l’avons annoncé, dans le cas d’une recherche sur le web, on combine le facteur PageRank avec d’autres facteurs. Par exemple, si, étant donné une requête, la similarité entre la requête et un document est ![]() , on pourra combiner cette valeur avec le PageRank
, on pourra combiner cette valeur avec le PageRank ![]() pour obtenir
pour obtenir
un indice global de pertinence ![]() pour
pour ![]() . Ainsi, au lieu de ne tenir compte que du contenu du document
. Ainsi, au lieu de ne tenir compte que du contenu du document
pour faire la recherche, on tient compte aussi de sa popularité relative sur le web !
Google tient compte des termes utilisés dans les liens. Par exemple, si je fais un hyperlien comme ceci Jobolo, alors la page cible (ici google.com) sera associée au terme « Jobolo ». À cause de la loi de Zipf, environ 95 % du texte sur le web est composé d’environ 10 000 mots.
Peut-on calculer le PageRank encore plus rapidement ?
L’algorithme PageRank, tel qu’on vient de le décrire, s’avère très coûteux. Il se trouve qu’on peut accélérer les calculs en tenant compte du fait que la majorité des liens sont faits au sein d’un même site web. On calcule alors initialement le PageRank par blocs pour ensuite, seulement, faire le véritable calcul. Cet algorithme plus rapide se nomme BlockRank.
Référence :
– S.D. Kamvar, et al., Exploiting the Block Structure of the Web for Computing PageRank, 2003.
[1] En fait, on devrait généralement considérer le web comme un graphe où les sommets peuvent être des pages web ou d’autres documents ou services.
[2] Lawrence Page, Sergey Brin, Rajeev Motwani, and Terry Winograd,
The PageRank Citation Ranking : Bringing Order to the Web, 1998.
[3] Les facteurs en question ne sont pas divulgués.
[4] En fait, il n’est pas nécessaire que la somme des composantes soit 1, mais c’est utile si on veut voir le problème comme une chaîne de Markov.
[5] On suppose qu’au moins une seule page n’a aucun lien vers une autre page.
[6] Même s’il existe des algorithmes ésotériques qui font un peu mieux.



![\left [ \begin{array}{lll}
0 & -1 & 1 \\
-1 & 0 & 1\\
\frac{1}{2} & 1 & 0
\end{array} \right ]
\left [ \begin{array}{l}
x \\
y \\
z
\end{array} \right ] = \left [ \begin{array}{l}
x \\
y \\
z
\end{array} \right ]. \left [ \begin{array}{lll}
0 & -1 & 1 \\
-1 & 0 & 1\\
\frac{1}{2} & 1 & 0
\end{array} \right ]
\left [ \begin{array}{l}
x \\
y \\
z
\end{array} \right ] = \left [ \begin{array}{l}
x \\
y \\
z
\end{array} \right ].](local/cache-TeX/dce843eb5c2fd38985f96748c80c3847.png)
![\left [ \begin{array}{lllllll}
x_1 & x_2 & x_3 & x_4 & x_5 & x_6
\end{array} \right ]
\left [ \begin{array}{llllll}
0 & \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 & 0 \\
\frac{1}{3} & 0 & 0 & 0 & \frac{1}{3} & \frac{1}{3} \\
1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0
\end{array} \right ]
=\left [ \begin{array}{lllllll}
x_1 & x_2 & x_3 & x_4 & x_5 & x_6
\end{array} \right ].
\left [ \begin{array}{lllllll}
x_1 & x_2 & x_3 & x_4 & x_5 & x_6
\end{array} \right ]
\left [ \begin{array}{llllll}
0 & \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 & 0 \\
\frac{1}{3} & 0 & 0 & 0 & \frac{1}{3} & \frac{1}{3} \\
1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0
\end{array} \right ]
=\left [ \begin{array}{lllllll}
x_1 & x_2 & x_3 & x_4 & x_5 & x_6
\end{array} \right ].](local/cache-TeX/c47556067c58a4a192b1c5ca89c83b7f.png)
![\left [ \begin{array}{llll}
0 & 0 & 1 & 0 \\
\frac{1}{3} & 0 & \frac{1}{3} &\frac{1}{3} \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0
\end{array} \right ].
\left [ \begin{array}{llll}
0 & 0 & 1 & 0 \\
\frac{1}{3} & 0 & \frac{1}{3} &\frac{1}{3} \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0
\end{array} \right ].](local/cache-TeX/3741eb8f1b480e8664216ba55f519e04.png)
![\left [ \begin{array}{llll}
\frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4}
\end{array} \right ]
\left [ \begin{array}{llll}
0 & 0 & 1 & 0 \\
\frac{1}{3} & 0 & \frac{1}{3} &\frac{1}{3} \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0
\end{array} \right ]^{10000} =
\left [ \begin{array}{llll}
0.5 & 0 & 0.5 & 0
\end{array} \right ].
\left [ \begin{array}{llll}
\frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4}
\end{array} \right ]
\left [ \begin{array}{llll}
0 & 0 & 1 & 0 \\
\frac{1}{3} & 0 & \frac{1}{3} &\frac{1}{3} \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0
\end{array} \right ]^{10000} =
\left [ \begin{array}{llll}
0.5 & 0 & 0.5 & 0
\end{array} \right ].](local/cache-TeX/0375cf1e7cd4befd2a75fb2e3aaf61fa.png)
![\left [ \begin{array}{llllll}
\frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} \\
\frac{q}{3}+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} \\
q+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} \\
q+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} \\
q+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} \\
q+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6}
\end{array} \right ] \left [ \begin{array}{llllll}
\frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} \\
\frac{q}{3}+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} & \frac{q}{3}+\frac{1-q}{6} \\
q+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} \\
q+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} \\
q+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} \\
q+\frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6} & \frac{1-q}{6}
\end{array} \right ]](local/cache-TeX/411e2b2ab45bb68a3500a24775746c27.png)

